题目内容
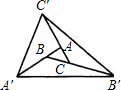 如图,分别延长△ABC的三边AB,BC,CA至A′,B′,C′,使得AA′=3AB,BB′=3BC,CC′=3AC.若S△ABC=1,则S△A′B′C′等于
如图,分别延长△ABC的三边AB,BC,CA至A′,B′,C′,使得AA′=3AB,BB′=3BC,CC′=3AC.若S△ABC=1,则S△A′B′C′等于
- A.18
- B.19
- C.24
- D.27
B
分析:连接AB′,BC′,CA′,利用已知条件求出S△C′CB′=2S△ACB′=6,S△AC′A=6,S△BA′B′=6,然后即可得出S△A′B′C′.
解答: 解:连接AB′,BC′,CA′,
解:连接AB′,BC′,CA′,
∵S△ABC=1,BB′=3BC,
∴S△ACB′=2.
∴S△C′CB′=3S△ACB′=6,
由∵S△ABC=1,
∴S△ABC′=2,
∴S△AC′A′=3S△ABC′=6.
同理,S△A′B′C′S△BA′B′=6,
∴S△A′B′C′=6+6+6+1=19.
故选B.
点评:此题主要考查学生对三角形面积的计算,解答此题的关键是连接AB′,BC′,CA′,利用两三角形同高这一特点,求出三角形C′CB′的面积等于6.此题有一定难度,属于难题.
分析:连接AB′,BC′,CA′,利用已知条件求出S△C′CB′=2S△ACB′=6,S△AC′A=6,S△BA′B′=6,然后即可得出S△A′B′C′.
解答:
 解:连接AB′,BC′,CA′,
解:连接AB′,BC′,CA′,∵S△ABC=1,BB′=3BC,
∴S△ACB′=2.
∴S△C′CB′=3S△ACB′=6,
由∵S△ABC=1,
∴S△ABC′=2,
∴S△AC′A′=3S△ABC′=6.
同理,S△A′B′C′S△BA′B′=6,
∴S△A′B′C′=6+6+6+1=19.
故选B.
点评:此题主要考查学生对三角形面积的计算,解答此题的关键是连接AB′,BC′,CA′,利用两三角形同高这一特点,求出三角形C′CB′的面积等于6.此题有一定难度,属于难题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
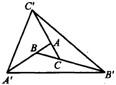 4、如图,分别延长△ABC的三边AB,BC,CA至A′,B′,C′,使得AA′=3AB,BB′=3BC,CC′=3AC.若S△ABC=1,则S△A′B′C′等于( )
4、如图,分别延长△ABC的三边AB,BC,CA至A′,B′,C′,使得AA′=3AB,BB′=3BC,CC′=3AC.若S△ABC=1,则S△A′B′C′等于( )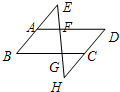 19、如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.
19、如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.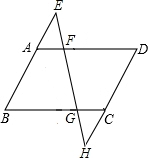 如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.
如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.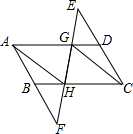 如图,分别延长?ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.求证:CG∥AH.
如图,分别延长?ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.求证:CG∥AH.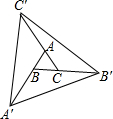 如图,分别延长△ABC的三边AB、BC、CA至A′、B′、C′,使得AA′=3AB,BB′=3BC,CC′=3AC,
如图,分别延长△ABC的三边AB、BC、CA至A′、B′、C′,使得AA′=3AB,BB′=3BC,CC′=3AC,