题目内容
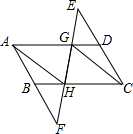 如图,分别延长?ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.求证:CG∥AH.
如图,分别延长?ABCD的边CD,AB到E,F,使DE=BF,连接EF,分别交AD,BC于G,H,连结CG,AH.求证:CG∥AH.分析:首先根据全等三角形的判定定理ASA证得:△DEG≌△BFH,根据对应边相等证得DG=BH,从而得出AG=CH,判断出四边形AGCH是平行四边形,继而得出结论.
解答:解:∵四边形ABCD是平行四边形,
∴AE∥CF,∠ADC=∠ABC,
∴∠E=∠F,∠EDG=∠FBH,
在△DEG与△BFH中,∵
,
∴△DEG≌△BFH(ASA),
∴DG=BH,
∴AD-DG=BC-BH,即CH=AG,
又∵AG∥CH,
∴四边形AGCH为平行四边形,
∴CG∥AH.
∴AE∥CF,∠ADC=∠ABC,
∴∠E=∠F,∠EDG=∠FBH,
在△DEG与△BFH中,∵
|
∴△DEG≌△BFH(ASA),
∴DG=BH,
∴AD-DG=BC-BH,即CH=AG,
又∵AG∥CH,
∴四边形AGCH为平行四边形,
∴CG∥AH.
点评:本题考查了平行四边形的性质、全等三角形的判定与性质,一般证明两直线平行都会寻找内错角、同位角或同旁内角,本题的解答确是利用的平行四边形,同学们注意掌握这一种思路.

练习册系列答案
相关题目
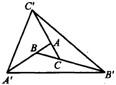 4、如图,分别延长△ABC的三边AB,BC,CA至A′,B′,C′,使得AA′=3AB,BB′=3BC,CC′=3AC.若S△ABC=1,则S△A′B′C′等于( )
4、如图,分别延长△ABC的三边AB,BC,CA至A′,B′,C′,使得AA′=3AB,BB′=3BC,CC′=3AC.若S△ABC=1,则S△A′B′C′等于( )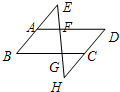 19、如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.
19、如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.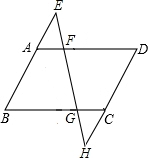 如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.
如图,分别延长?ABCD的边BA、DC到点E、H,使得AE=AB,CH=CD,连接EH,分别交AD、BC于点F、G.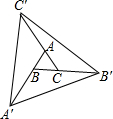 如图,分别延长△ABC的三边AB、BC、CA至A′、B′、C′,使得AA′=3AB,BB′=3BC,CC′=3AC,
如图,分别延长△ABC的三边AB、BC、CA至A′、B′、C′,使得AA′=3AB,BB′=3BC,CC′=3AC,