题目内容
【题目】如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…An,….则顶点M2014的坐标为_______.
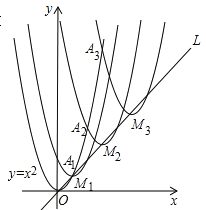
【答案】(4027,4027).
【解析】
试题解析:M1(a1,a1)是抛物线y1=(x-a1)2+a1的顶点,
抛物线y=x2与抛物线y1=(x-a1)2+a1相交于A1,
得x2=(x-a1)2+a1,
即2a1x=a12+a1,
x=![]() (a1+1).
(a1+1).
∵x为整数点
∴a1=1,
M1(1,1);
M2(a2,a2)是抛物线y2=(x-a2)2+a2=x2-2a2x+a22+a2顶点,
抛物线y=x2与y2相交于A2,
x2=x2-2a2x+a22+a2,
∴2a2x=a22+a2,
x=![]() (a2+1).
(a2+1).
∵x为整数点,
∴a2=3,
M2(3,3),
M3(a3,a3)是抛物线y2=(x-a3)2+a3=x2-2a3x+a32+a3顶点,
抛物线y=x2与y3相交于A3,
x2=x2-2a3x+a32+a3,
∴2a3x=a32+a3,
x=![]() (a3+1).
(a3+1).
∵x为整数点
∴a3=5,
M3(5,5),
∴点M2014,两坐标为:2014×2-1=4027,
∴M2014(4027,4027).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目