��Ŀ����
����Ŀ��ij�����Կ����ڼ䣬�Ŷ��շѷ������£�������30��ʱ���˾��շ�120Ԫ������30���Ҳ�����m��30��m��100����ʱ��ÿ����1�ˣ��˾��շѽ���1Ԫ������m��ʱ���˾��շѶ�����m��ʱ�ı����辰��Ӵ���x���ο͵�ij�Ŷӣ���ȡ�ܷ���ΪyԪ��
��1����y����x�ĺ�������ʽ��
��2�����㹤����Ա���֣����Ӵ�ij�Ŷ���������һ������ʱ�����������������������ȡ���ܷ��÷���������һ����Ϊ������ȡ���ܷ��������Ŷ������������Ӷ����ӣ���m��ȡֵ��Χ��
���𰸡�
��1���⣺y= 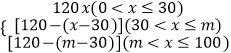 ��
��
��2���⣺�ɣ�1����֪��0��x��30��m��x��100������ֵy��������x�����Ӷ����ӣ�
��30��x��mʱ��y=��x2+150x=����x��75��2+5625��
��a=��1��0��
��x��75ʱ��y����x���Ӷ����ӣ�
��Ϊ������ȡ���ܷ��������Ŷ������������Ӷ����ӣ�
��30��m��75
����������1�������շѱ�����0��x��30��30��x��m��m��x��100�ֱ����y��x�Ĺ�ϵ���ɣ���2���ɣ�1����֪��0��x��30��m��x��100������ֵy��������x�����Ӷ����ӣ�30��x��mʱ��y=��x2+150x=����x��75��2+5625�����ݶ��κ��������ʼ��ɽ�����⣮






