题目内容
甲、乙两人玩猜数字游戏，先由甲心中任想一个数字，记为a，再由乙猜甲刚才所想数字，把乙所猜数字记为b，且a，b分别取数字0，1，2，3，若a，b满足|a-b|≤1，则称甲、乙两人“心有灵犀”．现任意找两人玩这个游戏，得出他们“心有灵犀”的概率为
．
| 5 |
| 8 |
| 5 |
| 8 |
分析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与他们“心有灵犀”的情况，再利用概率公式求解即可求得答案．
解答：解：画树状图得：
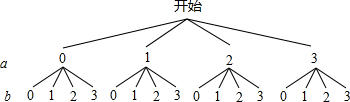
∵共有16种等可能的结果，a，b满足|a-b|≤1的有10种情况，
∴得出他们“心有灵犀”的概率为：
=
．
故答案为：
．
∵共有16种等可能的结果，a，b满足|a-b|≤1的有10种情况，
∴得出他们“心有灵犀”的概率为：
| 10 |
| 16 |
| 5 |
| 8 |
故答案为：
| 5 |
| 8 |
点评：本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
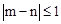，则称甲、乙两人“心有灵犀”。则甲、乙两人“心有灵犀”的概率是 .