题目内容
甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为a,再由乙猜甲刚才所想数字,把乙所猜数字记为b,且a、b分别取数字0、1、2,若a、b满足|a-b|≤1,则称甲、乙两人“心有灵犀”.现任意找两人玩这个游戏.(1)利用树状图或列表的方法(只选其中一种)表示出猜数字游戏可能出现的所有结果;
(2)求出他们“心有灵犀”的概率.
分析:(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,即可解答.
(2)根据上表的结果根据概率公式求出该事件的概率即可.
(2)根据上表的结果根据概率公式求出该事件的概率即可.
解答:解:(1)猜数字游戏可能出现的所有结果如下表所示:
(2)从如上表可看出:事件发生的所有可能的结果总数为9,“心有灵犀“的结果总数为7,因此其概率为
.
| 0 | 1 | 2 | |
| 0 | 0 | |-1| | |-2| |
| 1 | 1 | 0 | |-1| |
| 2 | 2 | 1 | 0 |
| 7 |
| 9 |
点评:本题主要考查概率的概念和求法,用树状图或表格表达事件出现的可能性是求解概率的常用方法.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
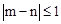 ,则称甲、乙两人“心有灵犀”。则甲、乙两人“心有灵犀”的概率是 .
,则称甲、乙两人“心有灵犀”。则甲、乙两人“心有灵犀”的概率是 .