题目内容
如图，△ABC是等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连接BD，交AC于F．猜想AC与BD的位置关系，并证明你的结论．
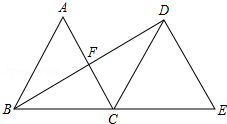
答：垂直．
证明：∵△DCE由△ABC平移而成，
∴△DCE≌△ABC，
∴△DCE是等边三角形，
∴BC=CD，∠ACB=∠DCE=60°，
∴∠ACD=180°-120°=60°，
∴∠ACD=∠ACB，
∵BC=CD，
∴AC⊥BD．
证明：∵△DCE由△ABC平移而成，
∴△DCE≌△ABC，
∴△DCE是等边三角形，
∴BC=CD，∠ACB=∠DCE=60°，
∴∠ACD=180°-120°=60°，
∴∠ACD=∠ACB，
∵BC=CD，
∴AC⊥BD．
练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
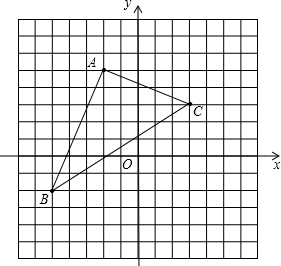
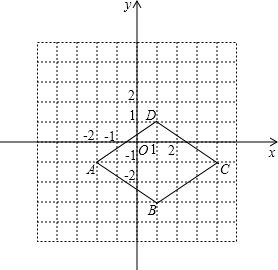
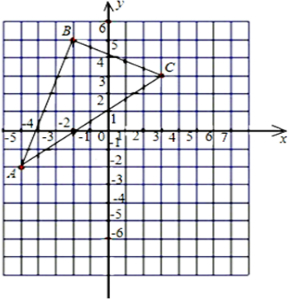
，0），C（-2，4），
