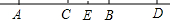题目内容
如图，C、D是线段AB上两点，已知AC：CD：DB=1：2：3，M、N分别为AC、DB的中点，且AB=18cm，求线段MN的长．
设AC、CD、DB的长分别为xcm、2xcm、3xcm，
则∵AC+CD+DB=AB，
∴x+2x+3x=18，解得：x=3cm，
∴AC=3cm，CD=6cm，DB=9cm，
∵M、N分别为AC、DB的中点，
∴MC=
，DN=
（3分）
∴MN=MC+CD+DN=
+6+
=12（5分）
答：MN的长为12cm．
则∵AC+CD+DB=AB，
∴x+2x+3x=18，解得：x=3cm，
∴AC=3cm，CD=6cm，DB=9cm，
∵M、N分别为AC、DB的中点，
∴MC=
| 3 |
| 2 |
| 9 |
| 2 |
∴MN=MC+CD+DN=
| 3 |
| 2 |
| 9 |
| 2 |
答：MN的长为12cm．
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
