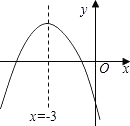��Ŀ����
����Ŀ����ͼ����ˮƽ�����A����һ������������з��������������·����һ�������ߣ��ڵ��������ΪB��������ֱ��AB�ϵ�C������Bһ�ࣩ��ֱ���ϰڷ��ǵ�Բ����Ͱ����ͼ����������Ͱ�ڣ���֪AB=4�ף�AC=3�ף�����������߶�OM=5�ף�Բ����Ͱ��ֱ��CDΪ0.5�ף���Ϊ0.3�ף�����������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ���
��1����ͼ������ֱ������ϵ����������ߵĽ���ʽ��
��2�������ֱ�ڷ�7��Բ����Ͱʱ�������ܲ�������Ͱ�ڣ�
��3������ֱ�ڷ�Բ����Ͱ������ٸ�ʱ�������������Ͱ�ڣ�
���𰸡�
��1��
�⣺M��0��5����B��2��0����C��1��0����D�� ![]() ��0����
��0����
�������ߵĽ���ʽΪy=ax2+k��
�������߹���M�͵�B��
��k=5�� ![]() ��
��
�������߽���ʽΪ ![]() ��
��
��2��
�⣺��x=1ʱ��y= ![]() ����x=
����x= ![]() ʱ��y=
ʱ��y= ![]() ��
��
��P��1�� ![]() ����Q��
����Q�� ![]() ��
�� ![]() ��
��
����ֱ�ڷ�7��Բ����Ͱʱ��Ͱ��= ![]() ��7=2.1��
��7=2.1��
��2.1�� ![]() ��2.1��
��2.1�� ![]() ��
��
������������Ͱ�ڣ�
��3��
�⣺����ֱ�ڷ�Բ����Ͱm��ʱ�����������Ͱ�ڣ�
�����⣬�ã� ![]() ��0.3m��
��0.3m�� ![]() ��
��
��ã� ![]() ��m��
��m�� ![]() ��
��
��m������
��m��ֵΪ8��9��10��11��12��
�൱��ֱ�ڷ�Բ����Ͱ����12��ʱ�������������Ͱ�ڣ�
����������1���������ߵĶԳ���Ϊy�ᣬˮƽ����Ϊx�ᣬ����ƽ��ֱ������ϵ�������ʽ�������֪ȷ���������ϵ�����꣬�������ʽȷ�������ߵĽ���ʽ����2�����õ�x=1ʱ��y= ![]() ����x=1.5 ʱ��y=
����x=1.5 ʱ��y= ![]() ���ó�����ֱ�ڷ�5��Բ����Ͱʱ���ó�Ͱ�߽����Ƚϣ����ɵó��𰸣���3����ԲͰ��ֱ�������ԲͰ����Ե�������ֵ��ȷ��m�ķ�Χ������mΪ���������ó�m��ֵ�����ɵõ��������������Ͱ��ʱ����ֱ�ڷ�Բ����Ͱ������
���ó�����ֱ�ڷ�5��Բ����Ͱʱ���ó�Ͱ�߽����Ƚϣ����ɵó��𰸣���3����ԲͰ��ֱ�������ԲͰ����Ե�������ֵ��ȷ��m�ķ�Χ������mΪ���������ó�m��ֵ�����ɵõ��������������Ͱ��ʱ����ֱ�ڷ�Բ����Ͱ������
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�