题目内容
已知抛物线 .
.
(1)用配方法将 化成
化成 的形式;
的形式;
(2)将此抛物线向右平移1个单位,再向上平移2个单位,求平移后所得抛物线的解析式.
 .
.(1)用配方法将
 化成
化成 的形式;
的形式;(2)将此抛物线向右平移1个单位,再向上平移2个单位,求平移后所得抛物线的解析式.
(1)y=(x-2)2-3 .(2)y=(x-3)2-1=x2-6x+8
试题分析:(1)∵y=x2-4x+1 ∴y=x2-4x+4-4+1 y=(x-2)2-3 (2)由(1)得y=(x-2-1)2-3+2即y=(x-3)2-1 解:(1)

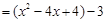
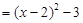 ............................................................. 2分
............................................................. 2分(2)∵抛物线
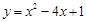 的顶点坐标为
的顶点坐标为 , ............................ 3分
, ............................ 3分∴平移后的抛物线的顶点坐标为
 . ...................................... 4分
. ...................................... 4分∴平移后所得抛物线的解析式为
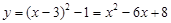 . 5分
. 5分点评:熟知二次函数图象平移时,上加下减,左加右减。即上下平移时,纵坐标加减,左右平移时,横坐标加减。这里注意的是;平移时一定要把二次函数的解析式化成顶点式形式,函数标准解析式化顶点式时;配方的原则是,一次项系数一半的平方比上二次项系数,此题的二次项为“1”,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
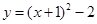 的最小值是( )
的最小值是( ) 与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形。
与x轴相交于A、B两点,与y轴相交于点C,连结BC,已知△BOC是等腰三角形。
 经过A(2,0)、B(0,-6)两点,其对称轴与
经过A(2,0)、B(0,-6)两点,其对称轴与 轴交于点C.
轴交于点C.

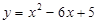 .
.  的形式;
的形式;  取何值时,
取何值时, 随
随