Question

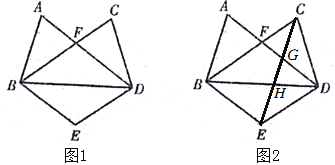
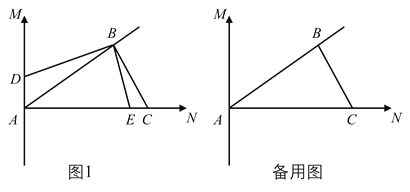
【题目】如图1，直线，AB平分，过点B作交AN于点C；动点E、D同时从A点出发，其中动点E以的速度沿射线AN方向运动，动点D以的速度运动；已知，设动点D，E的运动时间为t．

试求的度数；

当点D在射线AM上运动时满足：：3，试求点D，E的运动时间t的值；

当动点D在直线AM上运动，E在射线AN运动过程中，是否存在某个时间t，使得与全等？若存在，请求出时间t的值；若不存在，请说出理由．

Answer 1

【答案】（1）∠ACB=45°；（2）t= s或12s；（3）存在． t的值为2s或6s．

【解析】

（1）根据角平分线的定义、直角三角形的锐角互余即可解决问题．
（2）作BH⊥AC于H，BG⊥AM于G．由BA平分∠MAN，推出BG=BH，由S△ADB：S△BEC=2：3，AD=t，AE=2t，可得tBG： （6-2t）BH=2：3，解方程即可解决问题．
（3）存在．由BA=BC，∠BAD=∠BCE=45°，可知当AD=EC时，△ADB≌△CEB，列出方程即可解决问题．

（1）如图1中，

∵AM⊥AN，
∴∠MAN=90°，
∵AB平分∠MAN，
∴∠BAC=45°，
∵CB⊥AB，
∴∠ABC=90°，
∴∠ACB=45°．
（2）如图2中，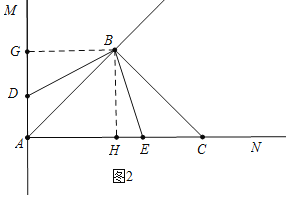

①当E在线段AC上时，作BH⊥AC于H，BG⊥AM于G．
∵BA平分∠MAN，
∴BG=BH，
∵S△ADB：S△BEC=2：3，AD=t，AE=2t，
∴tBG： （6-2t）BH=2：3，
∴t=s．
②当点E运动到AC延长线上，同法可得t=12时，也满足条件！
∴当t= s或12s时，满足S△ADB：S△BEC=2：3．
（3）存在．∵BA=BC，∠BAD=∠BCE=45°，
∴当AD=EC时，△ADB≌△CEB，
∴t=6-2t，
∴t=2s，
∴t=2s时，△ADB≌△CEB．
当D在MA延长线上时，2t-6=t，t=6s，
综上所述，满足条件的t的值为2s或6s．