Question

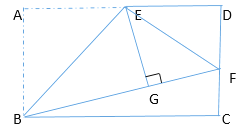
【题目】如图，在长方形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于F，连接EF，若AB=4,若BC=6,则DF的长为_______ .

Answer 1

【答案】

【解析】

利用翻折不变性，根据HL可以证明Rt△EDF≌Rt△EGF（HL），推出DF=FG，设DF=x，则BF=4+x，CF=4-x，在Rt△BCF中，根据勾股定理求出x即可.

解：∵E是AD的中点，

∴AE=DE，

∵△ABE沿BE折叠后得到△GBE，

∴AE=EG，AB=BG，

∴ED=EG，

∵在矩形ABCD中，

∴∠A=∠D=90°，

∴∠EGF=90°，

∵在Rt△EDF和Rt△EGF中，

∴Rt△EDF≌Rt△EGF（HL），

∴DF=FG，

设DF=x，则BF=4+x，CF=4-x，

在Rt△BCF中，，解得，则DF=.