题目内容
 如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=
如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=
- A.
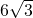
- B.
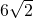
- C.
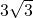
- D.
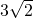
A
分析:根据垂径定理先求BC一半的长,再求BC的长.
解答: 解:设OA与BC相交于D点.
解:设OA与BC相交于D点.
∵AB=OA=OB=6
∴△OAB是等边三角形.
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD=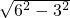 =3
=3
所以BC=6 .
.
故选A.
点评:本题的关键是利用垂径定理和勾股定理.
分析:根据垂径定理先求BC一半的长,再求BC的长.
解答:
 解:设OA与BC相交于D点.
解:设OA与BC相交于D点.∵AB=OA=OB=6
∴△OAB是等边三角形.
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD=
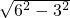 =3
=3
所以BC=6
 .
.故选A.
点评:本题的关键是利用垂径定理和勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
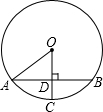 如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )
如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为( )| A、10 | B、8 | C、6 | D、4 |
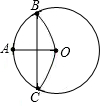 如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )A、6
| ||
B、6
| ||
C、3
| ||
D、3
|
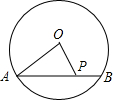 如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为
如图,⊙O的半径OA=5cm,若弦AB=8cm,P为AB上一动点,则点P到圆心O的最短距离为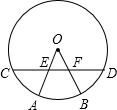 如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.
如图,⊙O的半径OA、OB分别交弦CD于点E、F,且CE=DF.请说明AE=BF.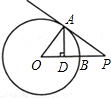 如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,
如图,⊙O的半径OA=3,P是⊙O外一点,OP交⊙O于点B,PB=2,PA=4,