题目内容
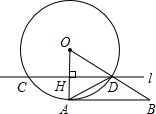 (2012•南平)如图,直线l与⊙O交于C、D两点,且与半径OA垂直,垂足为H,已知OD=2,∠O=60°,
(2012•南平)如图,直线l与⊙O交于C、D两点,且与半径OA垂直,垂足为H,已知OD=2,∠O=60°,(1)求CD的长;
(2)在OD的延长线上取一点B,连接AB、AD,若AD=BD,求证:AB是⊙O的切线.
分析:(1)由OA垂直于CD,利用垂径定理得到H为CD的中点,在直角三角形ODE中,由∠O=60°求出∠ODH=30°,根据30°角所对的直角边等于斜边的一半,由OD的长求出OH的长,再利用勾股定理求出HD的长,由CD=2HD即可求出CD的长;
(2)由OA=OD且∠O=60°,得到三角形OAD为等边三角形,可得出AD=OD,利用等边对等角得到一对角相等,再由AD=DB,利用等边对等角得到一对角相等,又这四个角之和为180°,等量代换可得出∠OAB为直角,即OA垂直于AB,即可得到AB为圆O的切线,得证.
(2)由OA=OD且∠O=60°,得到三角形OAD为等边三角形,可得出AD=OD,利用等边对等角得到一对角相等,再由AD=DB,利用等边对等角得到一对角相等,又这四个角之和为180°,等量代换可得出∠OAB为直角,即OA垂直于AB,即可得到AB为圆O的切线,得证.
解答:(1)解:∵OA⊥CD,
∴H为CD的中点,即CH=DH,
在Rt△OHD中,∠O=60°,
∴∠ODH=30°,又OD=2,
∴OH=
OD=1,
根据勾股定理得:HD=
=
,
则CD=2HD=2
;
(2)证明:∵OA=OD,∠O=60°,
∴△AOD为等边三角形,
∴∠OAD=∠ODA,
又AD=DB,
∴∠DAB=∠DBA,
∴∠OAD+∠ODA+∠DAB+∠DBA=2(∠ODA+∠DAB)=180°,
∴∠ODA+∠DAB=90°,即∠OAB=90°,
则AB为圆O的切线.
∴H为CD的中点,即CH=DH,
在Rt△OHD中,∠O=60°,
∴∠ODH=30°,又OD=2,
∴OH=
| 1 |
| 2 |
根据勾股定理得:HD=
| OD2-OH2 |
| 3 |
则CD=2HD=2
| 3 |
(2)证明:∵OA=OD,∠O=60°,
∴△AOD为等边三角形,
∴∠OAD=∠ODA,
又AD=DB,
∴∠DAB=∠DBA,
∴∠OAD+∠ODA+∠DAB+∠DBA=2(∠ODA+∠DAB)=180°,
∴∠ODA+∠DAB=90°,即∠OAB=90°,
则AB为圆O的切线.
点评:此题考查了切线的判定,垂径定理,勾股定理,含30°直角三角形的性质,等边三角形的判定与性质,以及等腰三角形的性质,利用了转化及等量代换的数学思想,其中切线的判定方法有两种:有点连接证明垂直;无点作垂线证明垂线段等于圆的半径.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 (2012•南平)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=68°,则∠BAC=
(2012•南平)如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D在⊙O上,∠ADC=68°,则∠BAC= (2012•南平)如图,在山坡AB上种树,已知∠C=90°,∠A=28°,AC=6米,则相邻两树的坡面距离AB≈
(2012•南平)如图,在山坡AB上种树,已知∠C=90°,∠A=28°,AC=6米,则相邻两树的坡面距离AB≈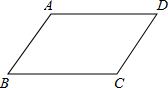 件中,选择添加一个恰当的条件.使四边形AECF是平行四边形,并予以证明,
件中,选择添加一个恰当的条件.使四边形AECF是平行四边形,并予以证明, 其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)
其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)