题目内容
【题目】正方形EFGH的顶点在边长为3的正方形ABCD边上,若AE=x,正方形EFGH的面积为y,则y与x的函数关系式为______.

【答案】y=2x2﹣6x+9
【解析】
由AAS证明△DHE≌△AEF,得出DE=AF=x,DH=AE=3-x,再根据勾股定理,求出EH2,即可得到y与x之间的函数关系式.
如图所示:
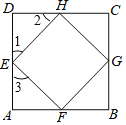
∵四边形ABCD是边长为3的正方形,
∴∠A=∠D=90°,AD=3.
∴∠1+∠2=90°,
∵四边形EFGH为正方形,
∴∠HEF=90°,EH=EF.
∴∠1+∠3=90°,
∴∠2=∠3,
在△AHE与△BEF中
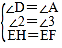 ,
,
∴△DHE≌△AEF(AAS),
∴DE=AF=x,DH=AE=3-x,
在Rt△AHE中,由勾股定理得:
EH2=DE2+DH2=x2+(3-x)2=2x2-6x+9;
即y=2x2-6x+9(0<x<3),
故答案为:y=2x2-6x+9.

练习册系列答案
相关题目