题目内容
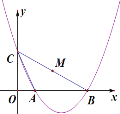
【题目】如图,抛物线![]() 交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A. n=![]() (m-
(m-![]() )2-
)2-![]() B. n=
B. n=![]() (m-
(m-![]() )2+
)2+![]()
C. n=![]() (m-
(m-![]() )2-
)2-![]() D. n=
D. n=![]() (m-
(m-![]() )2-
)2-![]()
【答案】D
【解析】
分析题意可知M点运动路径的形状和抛物线![]() 完全相同,相当于把原抛物线向右下方移动,求出点M的坐标,即可得到移动的方向和距离,即可得到n与m的关系式.
完全相同,相当于把原抛物线向右下方移动,求出点M的坐标,即可得到移动的方向和距离,即可得到n与m的关系式.
解:由抛物线![]() 可得C(0,2),解方程
可得C(0,2),解方程![]() 可求出B点坐标为(4,0),所以M(2,1),根据题意可知,M点的运动路径也是一个抛物线,相当于将抛物线
可求出B点坐标为(4,0),所以M(2,1),根据题意可知,M点的运动路径也是一个抛物线,相当于将抛物线![]() 向右移动2个单位长度,再向下移动1个单位长度.
向右移动2个单位长度,再向下移动1个单位长度.
![]() ,所以移动后的图像为
,所以移动后的图像为![]() ,
,
即:![]() ,
,
故选D.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目