题目内容
 (2012•山西)如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
(2012•山西)如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )分析:先根据半径OA长是6米,C是OA的中点可知OC=
OA=3,再在Rt△OCD中,利用勾股定理求出CD的长,根据锐角三角函数的定义求出∠DOC的度数,由S阴影=S扇形AOD-S△DOC即可得出结论.
| 1 |
| 2 |
解答: 解:连接OD,
解:连接OD,
∵弧AB的半径OA长是6米,C是OA的中点,
∴OC=
OA=
×6=3米,
∵∠AOB=90°,CD∥OB,
∴CD⊥OA,
在Rt△OCD中,
∵OD=6,OC=3,
∴CD=
=
=3
米,
∵sin∠DOC=
=
=
,
∴∠DOC=60°,
∴S阴影=S扇形AOD-S△DOC=
-
×3×3
=(6π-
)平方米.
故选C.
 解:连接OD,
解:连接OD,∵弧AB的半径OA长是6米,C是OA的中点,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=90°,CD∥OB,
∴CD⊥OA,
在Rt△OCD中,
∵OD=6,OC=3,
∴CD=
| OD2-OC2 |
| 62-32 |
| 3 |
∵sin∠DOC=
| CD |
| OD |
3
| ||
| 6 |
| ||
| 2 |
∴∠DOC=60°,
∴S阴影=S扇形AOD-S△DOC=
| 60×π×62 |
| 360 |
| 1 |
| 2 |
| 3 |
| 9 |
| 2 |
| 3 |
故选C.
点评:本题考查的是扇形的面积,根据题意求出∠DOC的度数,再由S阴影=S扇形AOD-S△DOC得出结论是解答此题的关键.

练习册系列答案
相关题目
 (2012•山西)如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )
(2012•山西)如图,直线AB∥CD,AF交CD于点E,∠CEF=140°,则∠A等于( )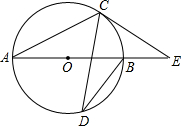 (2012•山西)如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( )
(2012•山西)如图,AB是⊙O的直径,C、D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于( ) (2012•山西)如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点B的坐标是
(2012•山西)如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点B的坐标是 (2012•山西)如图所示的工件的主视图是( )
(2012•山西)如图所示的工件的主视图是( )