题目内容
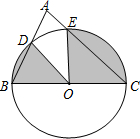 (2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为
(2012•浦口区一模)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E.若∠A=70°,BC=2,则图中阴影部分面积为| 7 |
| 18 |
| 7 |
| 18 |
分析:先根据三角形内角和定理得出∠ABC+∠ACB的度数,再由△OBD、△OCE是等腰三角形得出∠BDO+∠CEO的度数,由三角形内角和定理即可得出∠BOD+∠COD的度数,再根据扇形的面积公式即可得出结论.
解答:解:∵△ABC中,∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∵△OBD、△OCE是等腰三角形,
∴∠BDO+∠CEO=∠ABC+∠ACB=110°,
∴∠BOD+∠COE=360°-(∠BDO+∠CEO)-(∠ABC+∠ACB)=360°-110°-110°=140°,
∵BC=2,
∴OB=OC=1,
∴S阴影=
=
π.
故答案为:
π.
∴∠ABC+∠ACB=180°-70°=110°,
∵△OBD、△OCE是等腰三角形,
∴∠BDO+∠CEO=∠ABC+∠ACB=110°,
∴∠BOD+∠COE=360°-(∠BDO+∠CEO)-(∠ABC+∠ACB)=360°-110°-110°=140°,
∵BC=2,
∴OB=OC=1,
∴S阴影=
| 140×π×12 |
| 360 |
| 7 |
| 18 |
故答案为:
| 7 |
| 18 |
点评:本题考查的是扇形面积的计算,解答此类问题时往往用到三角形的内角和是180°这一隐藏条件.

练习册系列答案
相关题目
 (2012•浦口区一模)如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )
(2012•浦口区一模)如图,数轴上的A、B、C三点所表示的数分别为a、b、c,AB=BC,如果|a|>|c|>|b|,那么该数轴的原点O的位置应该在( )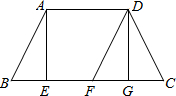 (2012•浦口区一模)如图,在等腰梯形ABCD中,AE是梯形的高,将△ABE沿BC方向平移,使点A与点D重合,得△DFG.若∠B=60°,当四边形ABFD是菱形时,
(2012•浦口区一模)如图,在等腰梯形ABCD中,AE是梯形的高,将△ABE沿BC方向平移,使点A与点D重合,得△DFG.若∠B=60°,当四边形ABFD是菱形时,
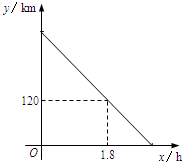 (2012•浦口区一模)一辆货车从A地出发以每小时100km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶1.8小时后,在距B地120km处与轿车相遇.图中线段表示货车离B地的距离y1与所用时间x的关系.根据函数图象探究:
(2012•浦口区一模)一辆货车从A地出发以每小时100km的速度匀速驶往B地,一段时间后,一辆轿车从B地出发沿同一条路匀速驶往A地.货车行驶1.8小时后,在距B地120km处与轿车相遇.图中线段表示货车离B地的距离y1与所用时间x的关系.根据函数图象探究: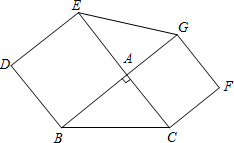 (2012•浦口区一模)提出问题:
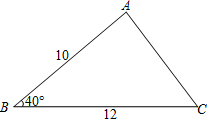
(2012•浦口区一模)提出问题: ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.
ABDE、ACFG,连接GE.求证:S△AEG=S△ABC.