题目内容
【题目】如图,已知抛物线经过点A(2,0),B(3,3)及原点O,顶点为C.

(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且以A,O,D,E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上第二象限内的动点,过点P作PM⊥x轴,垂足为M,是否存在点P使得以点P,M,A为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=x2-2x;(2)点P的坐标为(-![]() ,
,![]() )或(-3,15).
)或(-3,15).
【解析】
试题分析:(1)根据抛物线过A(2,0)及原点可设y=a(x-2)x,然后根据抛物线y=a(x-2)x过B(3,3),求出a的值即可;
(2)首先由A的坐标可求出OA的长,再根据四边形AODE是平行四边形,D在对称轴直线x=-1右侧,进而可求出D横坐标为:-1+2=1,代入抛物线解析式即可求出其横坐标;
(3)分△PMA∽△COB和△PMA∽△BOC表示出PM和AM,从而表示出点P的坐标,代入求得的抛物线的解析式即可求得t的值,从而确定点P的坐标.
试题解析:(1)根据抛物线过A(2,0)及原点,可设y=a(x-2)(x-0),
又∵抛物线y=a(x-2)x过B(3,3),
∴3(3-2)a=3,
∴a=1,
∴抛物线的解析式为y=(x-2)x=x2-2x;
(2)①若OA为对角线,则D点与C点重合,点D的坐标应为D(1,-1);
②若OA为平行四边形的一边,则DE=OA,∵点E在抛物线的对称轴上,
∴点E横坐标为1,
∴点D的横坐标为3或-1,代入y=x2-2x得D(3,3)和D(-1,3),
综上点D坐标为(1,-1),(3,3),(-1,3).
(3)∵点B(3,3)C(1,-1),
∴△BOC为直角三角形,∠COB=90°,且OC:OB=1:3,
①如图1,
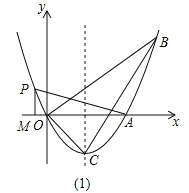
若△PMA∽△COB,设PM=t,则AM=3t,
∴点P(2-3t,t),
代入y=x2-2x得(2-3t)2-2(2-3t)=t,
解得t1=0(舍),t2=![]() ,
,
∴P(-![]() ,
,![]() );
);
②如图2,
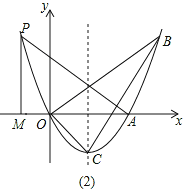
若△PMA∽△BOC,
设PM=3t,则AM=t,点P(2-t,3t),代入y=x2-2x得(2-t)2-2(2-t)=3t,
解得t1=0(舍),t2=5,
∴P(-3,15)
综上所述,点P的坐标为(-![]() ,
,![]() )或(-3,15).
)或(-3,15).

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】近年来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,为进一步普及环保和健康知识,我市某校举行了“建设宜居成都,关注环境保护”的知识竞赛,某班学生的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数 | 4 | 8 | 12 | 11 | 5 |
则该班学生成绩的众数和中位数分别是( )
A. 70分,80分 B. 80分,80分 C. 90分,80分 D. 80分,90分