题目内容
(2012•上海模拟)已知直线l经过正方形ABCD的顶点A,过点B和点D分别作直线l的垂线BM和DN,垂足分别为点M、点N,如果BM=5,DN=3,那么MN=
2或8
2或8
.分析:根据正方形的性质得出∠NAD=∠MBA,再利用全等三角形的判定得出△ABM≌△ADN,进而求出MN的值,注意分类讨论.
解答: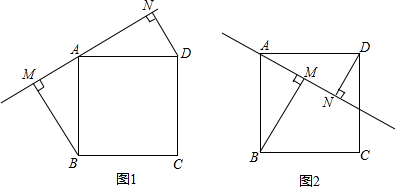 解:如图1,在正方形ABCD中,
解:如图1,在正方形ABCD中,
∵∠NAD+∠BAM=90°,∠ABM+∠BAM=90°,
∴∠NAD=∠MBA,
在△ABM和△ADN中,
∵
,
∴△ABM≌△ADN(AAS),
∴AM=DN=3,AN=BM=5,
∴MN=AM+AN=8,
如图2,在正方形ABCD中,
∵∠DAN+∠BAM=90°,∠ABM+∠BAM=90°,
∴∠NAD=∠MBA,
在△ABM和△ADN中,
∵
,
∴△ABM≌△ADN(AAS),
∴AM=DN=3,AN=BM=5,
∴MN=AN-AM=2,
综上所述:MN的值为2或8,
故答案为:2或8.
 解:如图1,在正方形ABCD中,
解:如图1,在正方形ABCD中,∵∠NAD+∠BAM=90°,∠ABM+∠BAM=90°,
∴∠NAD=∠MBA,
在△ABM和△ADN中,
∵
|
∴△ABM≌△ADN(AAS),
∴AM=DN=3,AN=BM=5,
∴MN=AM+AN=8,
如图2,在正方形ABCD中,
∵∠DAN+∠BAM=90°,∠ABM+∠BAM=90°,
∴∠NAD=∠MBA,
在△ABM和△ADN中,
∵
|
∴△ABM≌△ADN(AAS),
∴AM=DN=3,AN=BM=5,
∴MN=AN-AM=2,
综上所述:MN的值为2或8,
故答案为:2或8.
点评:此题主要考查了正方形的性质以及全等三角形的判定与性质等知识,根据已知正确画出图象进而得出两种情况是解题关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
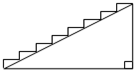 (2012•上海模拟)如图,如果在高为2m,坡度为1:2的楼梯上铺地毯,那么地毯的长度至少应截取( )
(2012•上海模拟)如图,如果在高为2m,坡度为1:2的楼梯上铺地毯,那么地毯的长度至少应截取( )