题目内容
【题目】在矩形ABCD中,AB=3,AD=4,点E为边AD上一动点,把△BAE沿直线BE折叠,恰好使得点A的对应点F落在矩形ABCD的对角线上,则△EBD的面积S= .
【答案】![]() 或
或![]() .
.
【解析】
试题解析:∵矩形ABCD,
∴∠A=90°,BD=![]()
当F在BD上时,如图1,设AE=x,
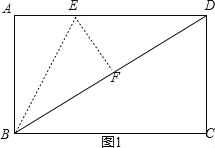
由翻折的性质得:EF=AE=x,BF=AB=3,
∴ED=4-x,∠EFD=∠A=90°,
∴FD=5-2=2,ED=4-x,
在Rt△EFD中,
x2+22=(4-x)2,
解得:x=![]() ,
,
∴ED=4-![]() =
=![]() ,
,
∴△EBD的面积S=![]() EDAB=
EDAB=![]() ×
×![]() ×3=
×3=![]() ;
;
当F在AC上时,如图2,
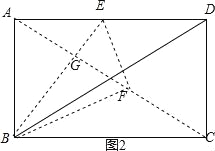
由翻折的性质得:BD垂直平分AF,AC=BD=5,
由射影定理得:AB2=AGAC,
∴AG=![]() ,
,
∴GC=AC-AG=![]() ,
,
∵AD∥BC,
∴∠EAG=∠ACB,
∵∠EGA=∠ABC=90°,
∴△AEG∽△CBG,
∴![]() ,
,
∴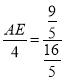 ,
,
∴AE=![]() ,
,
∴ED=4-![]() =
=![]() ,
,
∴△EBD的面积S=![]() EDAB=
EDAB=![]() ×
×![]() ×3=
×3=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目