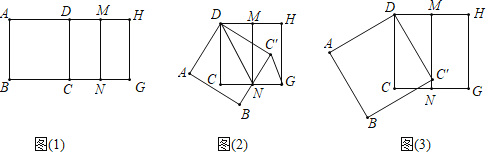
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]()
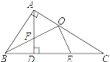
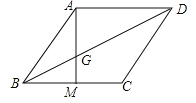
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 求的值;(
求的值;(![]() ,
,![]() 问要写出解答过程)
问要写出解答过程)
(3)当![]() 时,求
时,求![]() 的值.(直接写出结果)
的值.(直接写出结果)
【答案】(1)![]() =1;(2)
=1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() ,得到AC=2AB,又因为O为AC中点,推出AB=OC,利用AAS得出△ABF≌△COE,推出AF=CE,即可求出所求式子的比值;
,得到AC=2AB,又因为O为AC中点,推出AB=OC,利用AAS得出△ABF≌△COE,推出AF=CE,即可求出所求式子的比值;
(2)由![]() ,得到AB=AC,过A作AG平行于OE,交BC于点G,求出∠OEC=∠AGC,∠AFB=∠OEC,∠BAD=∠C=45°,利用AAS得出△AFB≌△CGA,推出AF=CG,得到E为CG的中点,即CE为CG的一半,即可求出所求式子的比.
,得到AB=AC,过A作AG平行于OE,交BC于点G,求出∠OEC=∠AGC,∠AFB=∠OEC,∠BAD=∠C=45°,利用AAS得出△AFB≌△CGA,推出AF=CG,得到E为CG的中点,即CE为CG的一半,即可求出所求式子的比.
(3)过A作AG平行于OE,交BC于点G,证△AFB∽△CGA,推出![]() ,再CG=2CE,代入求出即可.
,再CG=2CE,代入求出即可.
解:由![]() ,得到AC=2AB,
,得到AC=2AB,
又∵O为AC的中点,
∴AC=2OC,
∴AB=OC,
又∵在Rt△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD+∠ABC=90°,∠C+∠ABC=90°,
∴∠BAD=∠C,
又∵∠AFB=∠OBE+∠ADB,∠OEC=∠OBE+∠BOE,且∠ADB=∠BOE=90°,
∴∠AFB=∠OEC,
在△ABF和△COE中,
∴△ABF≌△COE(AAS),
∴AF=CE,
则![]() =1;
=1;
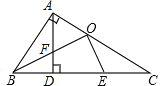
(2)过A作AG∥OE交BC于G,可得∠OEC=∠AGC,
由(1)得∠AFB=∠OEC,
∴∠AFB=∠AGC,
又∵![]() ,即AB=AC,∠BAC=90°,AD⊥BC,
,即AB=AC,∠BAC=90°,AD⊥BC,
∴∠BAD=∠C=45°,
在△AFB和△CGA中,
∴△AFB≌△CGA(AAS),
∴AF=CG,
![]()
![]()
![]()
(3)![]() ;
;
过A作AG平行于OE,交BC于点G,
由(1)(2)可知∠BAD=∠C,∠AFB=∠CGA,
∴△AFB∽△CGA,
∵![]()
∴![]()
又∵CG=2CE,
∴![]()
∴![]()

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?