题目内容
请先观察下列算式,再填空:32-12=8×1,52-32=8×2.
①72-52=8×
②92-(
③(
④132-(
…
(1)通过观察归纳,你知道上述规律的一般形式吗?请把你的猜想写出来.
(2)你能运用本章所学的平方差公式来说明你的猜想的正确性吗?
分析:(1)从上式中可以发现等式左边:两数的平方差,前一个数比后一个数大2;等式右边:前一个因数是8,后一个是等式左边两数的和除4,所以可写成:(n+2)2-n2=8×
(n≥1);
(2)运用平方差公式计算此式,证明它成立.
| (n+2)+n |
| 4 |
(2)运用平方差公式计算此式,证明它成立.
解答:解:
①3;
②7;
③11;
④11,6.
(1)(n+2)2-n2=8×
(n≥1);
(2)原式可变为(n+2+n)(n+2-n)=(n+2)2-n2=4n+4=8×
(n+2+n)=8×
.
①3;
②7;
③11;
④11,6.
(1)(n+2)2-n2=8×
| (n+2)+n |
| 4 |
(2)原式可变为(n+2+n)(n+2-n)=(n+2)2-n2=4n+4=8×
| 1 |
| 4 |
| (n+2)+n |
| 4 |
点评:(1)题的关键是找出各数之间的关系.
(2)题的关键是利用平方差公式计算此式,证明它成立.
(2)题的关键是利用平方差公式计算此式,证明它成立.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
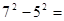 8× ; ②
8× ; ②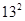 -( )
-( ) ;
; ;
;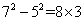 ;
;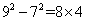 ;
;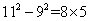 ;
;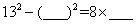 ;…
;…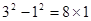 ,
, 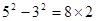 .
.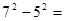 8×
; ②
8×
; ②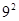 -( )
-( )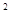 =8×4;
=8×4; -( )
-( )