题目内容
请先观察下列算式,再填空: ;
; ;
;
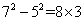 ;
;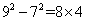 ;
;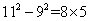 ;
;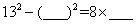 ;…
;…
(1)先填空,再通过观察归纳,你知道上述规律的一般形式吗?请把你的猜想写出来.
(2)你能运用所学的知识来说明你的猜想的正确性吗?
【答案】
(1)(2n+1)2-(2n-1)2=8n(n为正整数);(2)根据完全平方公式把(1)中发现的规律的等式左边去括号,再合并同类项即可.
【解析】
试题分析:(1)仔细分析所给式子的特征可得等式左边是连续奇数的平方差,等式右边是8的整数倍,根据这个规律求解即可;
(2)根据完全平方公式把(1)中发现的规律的等式左边去括号,再合并同类项即可.
(1)(2n+1)2-(2n-1)2=8n(n为正整数);
(2)∵左边=4n2+4n+1-(4n2-4n+1)=4n2+4n+1-4n2+4n-1=8n=右边
∴(2n+1)2-(2n-1)2=8n(n为正整数)成立.
考点:找规律-式子的变化
点评:解题此类问题的关键是仔细分析所给式子的特征得到规律,再把发现的规律应用于解题.

练习册系列答案
相关题目
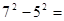 8× ; ②
8× ; ②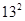 -( )
-( )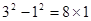 ,
, 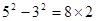 .
.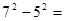 8×
; ②
8×
; ②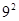 -( )
-( )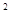 =8×4;
=8×4; -( )
-( )