题目内容
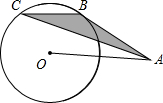 如图,A是半径为1的圆O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )
如图,A是半径为1的圆O外的一点,OA=2,AB是⊙O的切线,B是切点,弦BC∥OA,连接AC,则阴影部分的面积等于( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:连接OB,OC,易证:△BOC是等边三角形,且阴影部分的面积=△BOC的面积,据此即可求解.
解答: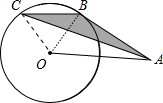 解:连接OB,OC,
解:连接OB,OC,
∵AB是圆的切线,
∴∠ABO=90°,
在直角△ABO中,OB=1,OA=2,
∴∠OAB=30°,∠AOB=60°,
∵OA∥BC,
∴∠COB=∠AOB=60°,且S阴影部分=S△BOC,
∴△BOC是等边三角形,边长是1,
∴S阴影部分=S△BOC=
×1×
=
.
故选A.
 解:连接OB,OC,
解:连接OB,OC,∵AB是圆的切线,
∴∠ABO=90°,
在直角△ABO中,OB=1,OA=2,
∴∠OAB=30°,∠AOB=60°,
∵OA∥BC,
∴∠COB=∠AOB=60°,且S阴影部分=S△BOC,
∴△BOC是等边三角形,边长是1,
∴S阴影部分=S△BOC=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
故选A.
点评:本题主要考查了三角形面积的计算,以及切割线定理,正确证明△BOC是等边三角形是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
如图,BC是半径为1的⊙O的弦,A为弧BC上一点,M、N分别为BD、AD的中点,则sin∠C的值等于( )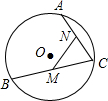

| A、AD | B、BC | C、MN | D、AC |
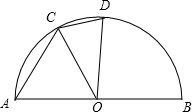 如图,
如图, |
| AB |
 |
| BC |
A、s=
| ||||
B、s=
| ||||
C、s=
| ||||
D、s=
|
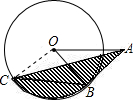 如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连接AC,则图中阴影部分的面积为
如图,A是半径为2的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,连接AC,则图中阴影部分的面积为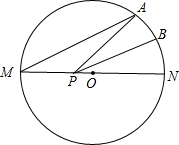 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )
如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,B为AN弧的中点,点P是直径MN上一个动点,则PA+PB的最小值为( )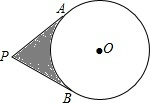 如图,P是半径为4的⊙O外一点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.
如图,P是半径为4的⊙O外一点,PA切⊙O于A,PB切⊙O于B,∠APB=60°.