题目内容
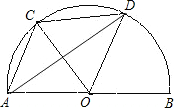
 如图,
如图, |
| AB |
 |
| BC |
A、s=
| ||||
B、s=
| ||||
C、s=
| ||||
D、s=
|
分析:根据三角形的面积公式S△COD=
CO•ODsin∠COD,因为ab都是圆的半径1,所以sin∠COD的值越大,面积越大进行解答.
| 1 |
| 2 |
解答:解:S△COD=
CO•ODsin∠COD,
∵CO=OD=1,
∴S△COD=
sin∠COD,
∵△AOC为等边三角形,
∴∠COB=120°,
∴0°<∠COD<120°,
∴当∠COD=90°时,sin∠COD最大,最大值是1,
∴△COD的面积S的最大值是
.
故选D.
| 1 |
| 2 |
∵CO=OD=1,
∴S△COD=
| 1 |
| 2 |
∵△AOC为等边三角形,
∴∠COB=120°,
∴0°<∠COD<120°,
∴当∠COD=90°时,sin∠COD最大,最大值是1,
∴△COD的面积S的最大值是
| 1 |
| 2 |
故选D.
点评:本题考查了三角形的面积的求法与锐角三角函数的增减性,熟记面积的求法并判断出∠COD的取值范围是解题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如图,
如图,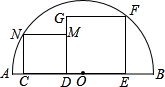 如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值.
如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值. 如图,AB是半径为10的⊙O的弦,OC⊥AB,垂足为点D,交⊙O于点C,且CD=2.求弦AB的长.
如图,AB是半径为10的⊙O的弦,OC⊥AB,垂足为点D,交⊙O于点C,且CD=2.求弦AB的长. 如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值.
如图,AB是半径为R的圆O的直径,四边形CDMN和DEFG都是正方形.其中C,D,E在AB上,F,N在半圆上.求证:两个正方形的面积之和为一定值.