题目内容
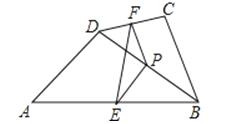
【题目】如图,矩形ABCD中,AB=12,BC=![]() ,点O是AB的中点,点P在AB的延长线上,且BP=6.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧,设运动的时间为t秒(
,点O是AB的中点,点P在AB的延长线上,且BP=6.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧,设运动的时间为t秒(![]() ).
).
(1)当t= 时,等边△EFG的边FG恰好经过点C时;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.

【答案】(1)t=2;
(2)当0≤t<2时,S= 4![]() t+16
t+16![]() ;当2≤t<6时,S=
;当2≤t<6时,S= ![]() t 2+6
t 2+6![]() t+
t+![]() ;当6≤t<8时,S= -8
;当6≤t<8时,S= -8![]() t+80
t+80![]() ;当8≤t<12时,S=
;当8≤t<12时,S=![]() t2-24
t2-24![]() t+144
t+144![]() ;
;
(3)存在5个这样的值,使△AOH是等腰三角形,即: t=6-2![]() 或t=6+2
或t=6+2![]() 或t=4或t=8或t=0.
或t=4或t=8或t=0.
【解析】试题分析:(1)当边FG恰好经过点C时,∠CFB=60°,BF=6-t,在Rt△CBF中,解直角三角形可求t的值;(2)按照等边△EFG和矩形ABCD重叠部分的图形特点,分为0≤t<2,2≤t<6,6≤t<8,8≤t<12四种情况,分别写出函数关系式;(3)存在.当△AOH是等腰三角形时,分为AH=AO=6,HA=HO,OH=OA三种情况,分别画出图形,根据特殊三角形的性质,列方程求t的值.
试题解析:(1)当边FG恰好经过点C时,∠CFB=60°,BF=6t,
在Rt△CBF中,BC=2![]() ,
,
∴tan∠CFB=![]() ,
,
∴tan60°=![]() ,
,
∴![]() =
=![]() ,
,
∴t=4,
∴当边FG恰好经过点C时,时间为t=4,
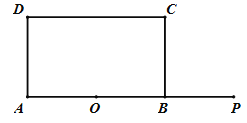
(2)如图1,
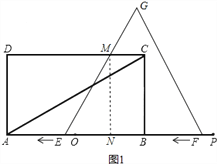
过点M作MN⊥AB,
①当0t<2时,如图1,
∵tan60°=![]() =
=![]() =
=![]() ,
,
∴NE=4,
∵EB=6+t,NB=6+t4=2+t,
∴MC=2+t,
∴S= (MC+EB)×BC=
![]() (2+t+6+t)×4
(2+t+6+t)×4![]() =4
=4![]() t+16
t+16![]() ;
;
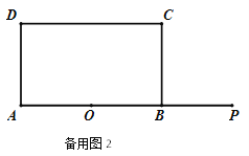
②当2t<6时,如图2,
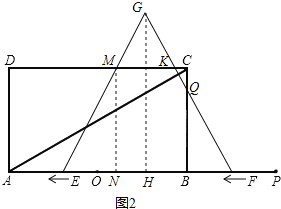
∵MN=4![]() ,EF=OP=12,
,EF=OP=12,
∴GH=12×![]() =6
=6![]() ,
,
∴![]() =
=![]() ,
,
∴MK=4,
∵EB=6+t,BF=6t,BQ=![]() ,
,
∴BQ=![]() (6t),CQ=4
(6t),CQ=4![]() BQ=
BQ=![]() t2
t2![]() .
.
∴S=S梯形MKFES△QBF=![]() (MK+EF)×MN
(MK+EF)×MN![]() BF×BQ==
BF×BQ==![]() t2+6
t2+6![]() t+14
t+14![]() ;
;
③如图3,
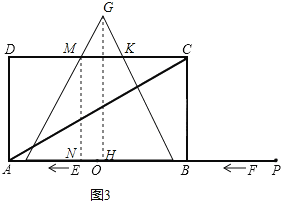
当6t<8时,
∵MN=4![]() ,EF=122(t6)=242t,
,EF=122(t6)=242t,
∴GH=(242t)×![]() =
=![]() (12t),
(12t),
∴![]() =
=![]() ,
,
∴MK=162t,
∴S=![]() (MK+EF)×MN=
(MK+EF)×MN=![]() (162t+242t)×4
(162t+242t)×4![]() =8
=8![]() t+80
t+80![]() ;
;
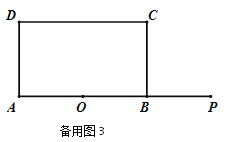
④如图4,
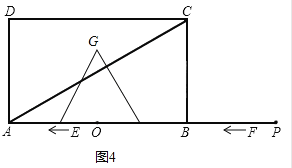
当8t<12时,
∵EF=242t,高为:EF×sin60°=![]() EF=
EF=![]() (242t)
(242t)
S=![]() EF×
EF×![]() EF=
EF=![]() (242t) 2 =
(242t) 2 =![]() t224
t224![]() t+144
t+144![]()
(3)存在,理由如下:
在Rt△ABC中,tan∠CAB=![]() =
=![]() ,
,
∴∠CAB=30°.
又∵∠HEO=60°,
∴∠HAE=∠AHE=30°.
∴AE=HE=6t或t6.
(Ⅰ)当AH=AO=6时,如图5,
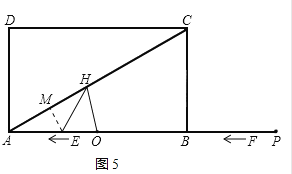
过点E作EM⊥AH于M,则AM=![]() AH=3.
AH=3.
在Rt△AME中,cos∠MAE=![]() ,
,
∴AE=2![]() ,
,
即6t=2![]() 或t6=2
或t6=2![]() ,t=62
,t=62或6+2
![]() .
.
(Ⅱ)当HA=HO时,如图6,
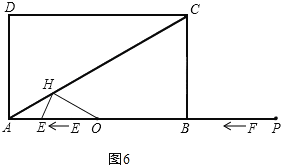
则∠HOA=∠HAO=30°,
又∵∠HEO=60°,
∴∠EHO=90°.
∴EO=2HE=2AE.
又∵AE+EO=6,
∴AE+2AE=6.
∴AE=2.
即6t=2或t6=2,
t=4或8.
(Ⅲ)当OH=OA时,如图7,
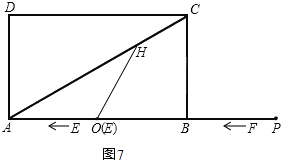
则∠OHA=∠OAH=30°,
∴∠HOB=60°=∠HEB.
∴点E和O重合,
∴AE=6.
即6t=6或t6=6,
t=12(舍去)或t=0.
综上所述,存在5个这样的值,使△AOH是等腰三角形,即:t=62![]() 或t=6+2
或t=6+2![]() 或t=4或t=8或t=0.
或t=4或t=8或t=0.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案