题目内容
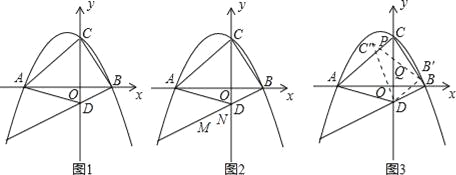
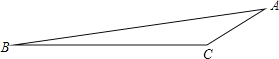
【题目】)如图,在△ABC中,∠C=150°,AC=4,tanB=![]() .
.
(1)求BC的长;
(2)利用此图形求tan15°的值.
【答案】(1)16-2![]() ;(2)2-
;(2)2-![]()
【解析】试题分析:(1)过A作AD⊥BC,交BC的延长线于点D,由含30°的直角三角形性质得AD=![]() AC=2,由三角函数求出CD=2
AC=2,由三角函数求出CD=2![]() ,在Rt△ABD中,由三角函数求出BD=16,即可得出结果;
,在Rt△ABD中,由三角函数求出BD=16,即可得出结果;
(2)在BC边上取一点M,使得CM=AC,连接AM,求出∠AMC=∠MAC=15°,tan15°=tan∠AMD=![]() 即可得出结果.
即可得出结果.
试题解析:(1)过A作AD⊥BC,交BC的延长线于点D,如图1所示:
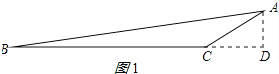
在Rt△ADC中,AC=4,
∵∠C=150°,
∴∠ACD=30°,
∴AD=![]() AC=2,
AC=2,
CD=ACcos30°=4×![]() =2
=2![]() ,
,
在Rt△ABD中,tanB=![]() ,
,
∴BD=16,
∴BC=BD-CD=16-2![]() ;
;
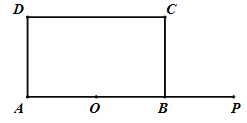
(2)在BC边上取一点M,使得CM=AC,连接AM,如图2所示:
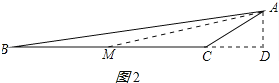
∵∠ACB=150°,
∴∠AMC=∠MAC=15°,
tan15°=tan∠AMD=![]() .
.

【题目】八达岭森林体验中心,由八达岭森林体验馆和450公顷的户外体验区构成。森林体验馆包括"八达岭森林变迁"、"八达岭森林大家族"、"森林让生活更美好"等展厅,户外游憩体验系统根据森林生态旅游最新理念,采取少设施、设施集中的点线布局模式,突破传统的"看风景"旅游模式,强调全面体验森林之美。
在室内展厅内,有这样一个可以动手操作体验的仪器,如图小明在社会大课堂活动中,记录了这样一组数字:

交通 工具 | 行驶100公里的碳足迹(Kg) | 100公里碳中 和树木棵树 |
飞机 | 13.9 | 0.06 |
小轿车 | 22.5 | 0.10 |
公共汽车 | 1.3 | 0.005 |
根据以上材料回答问题:
A,B两地相距300公里,小轿车以90公里/小时的速度从A地开往B地;公共汽车以60公里/小时的速度从B开往A地,两车同时出发相对而行,两车在C地相遇,相遇后继续前行到达各自的目的地。
(1)多少小时后两车相遇?
(2)小轿车和公共汽车分别到达目的地,计算小轿车的碳足迹为多少?公共汽车的碳中和树木棵数为多少?
(3)根据观察或计算说明,为了减少环境污染,我们应该选择哪种交通工具出行更有利于环保呢?