题目内容
(1)阅读材料:设一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则两根与方程系数之间有如下关系:x1+x2=-
,x1•x2=
.
根据该材料:已知x1、x2是方程x2+6x+3=0的两实数根,求
+
的值.
(2)已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,当0<x1<1,2<x2<3时,试判断y1与y2的大小关系.
| b |
| a |
| c |
| a |
根据该材料:已知x1、x2是方程x2+6x+3=0的两实数根,求
| x2 |
| x1 |
| x1 |
| x2 |
(2)已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
| x | … | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 2 | 1 | 2 | … |
分析:(1)根据根与系数的关系得出x1+x2=-
=-6,x1•x2=
=3,进而将原式变形求出即可;
(2)根据图表得出2<y1<5,1<y2<2,即可得出答案.
| b |
| a |
| c |
| a |
(2)根据图表得出2<y1<5,1<y2<2,即可得出答案.
解答:解;(1)∵x1、x2是方程x2+6x+3=0的两实数根,
∴x1+x2=-
=-6,x1•x2=
=3,
∴
+
=
=
=
=10;
(2)根据图表可得出:∵当0<x1<1时,2<y1<5,当2<x2<3时,1<y2<2,
∴y1>y2.
∴x1+x2=-
| b |
| a |
| c |
| a |
∴
| x2 |
| x1 |
| x1 |
| x2 |
| ||||
| x1x2 |
| (x1+x2)2-2x1x2 |
| x 1x2 |
| 36-2×3 |
| 3 |
(2)根据图表可得出:∵当0<x1<1时,2<y1<5,当2<x2<3时,1<y2<2,
∴y1>y2.
点评:此题主要考查了根与系数的关系以及利用图表得出正确数据信息,利用已知得出2<y1<5,1<y2<2是解题关键.

练习册系列答案
相关题目
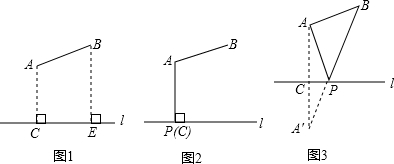
 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=