题目内容
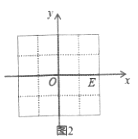
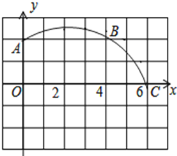
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点
A(0,2),B(4,2)C(6,0),解答下列问题:
(1)请在图中确定该圆弧所在圆心D点的位置,则D点坐标为___ ___;
(2)连结AD,CD,求⊙D的半径(结果保留根号);
(3)若把扇形DAC围成一个圆锥,求围成圆锥的底面半径(结果保留根号).
【答案】(1) D点坐标为(2,-2);(2)2![]() ;(3)
;(3)![]() .
.
【解析】
(1)由圆心在AB和BC的垂直平分线上,可得出D点的位置;
(2)过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,利用勾股定理可求得AD的长,即可得出半径;
(3) 求得弧长,除以2π即为圆锥的底面半径.
(1)如图1,作出线段AB和BC的垂直平分线的交点即为所求的D点,
可知D点坐标为(2,-2),
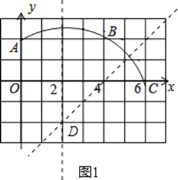
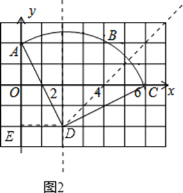
(2)如图2,过点D作DE⊥y轴,交y轴于点E,在Rt△ADE中,AE=2+2=4,DE=2,由勾股定理可求得AD=2![]() ,即⊙D的半径为2
,即⊙D的半径为2![]() ;
;
(3)如图2,连接AC,在Rt△AOC中,AO=2,OC=6,由勾股定理可求得AC=2![]() ,
,
在△ADC中,AD2+CD2=40=AC2,
∴∠ADC=90°,
∴设圆锥的底面半径为r,则![]() ,
,
![]() ,
,
∴r=![]() .
.

练习册系列答案
相关题目
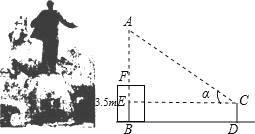
【题目】农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下.请你计算出铜像的高(结果精确到0.1m)
实习报告2003年9月25日
题目1 | 测量底部可以到达的铜像高 | |||
| ||||
测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
BD的长 | 12.3m | 11.7m | ||
测倾器CD的高 | 1.32m | 1.28m | ||
倾斜角 | α=30°56' | α=31°4' | ||
计 算 | ||||
结果 | ||||