题目内容
【题目】如图,在平面直角坐标系中,四边形OABC是正方形,点A的坐标是(4,0),P为边AB上一点,∠CPB=60°,沿CP折叠正方形OABC,折叠后,点B落在平面内的点B′处,则点B′的坐标为( )

A. (2,2![]() ) B. (
) B. (![]() ,2-
,2-![]() ) C. (2,4-2
) C. (2,4-2![]() ) D. (
) D. (![]() ,4-2
,4-2![]() )
)
【答案】C
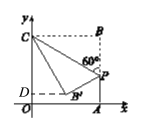
【解析】如下图,过点B′作B′D⊥OC于点D,由折叠的性质结合已知条件可得B′C=BC=OA=4,∠B′CP=∠BCP=90°-60°=30°,由此可得∠DCB′=30°,从而结合已知条件可解得B′D和OD的长,由此即可得到点B的坐标.
如下图,过点B′作B′D⊥OC于点D,
∵四边形OABC是正方形,点A的坐标为(4,0),
∴BC=OC=OA=4,∠B=∠BCO=90°,
∵∠CPB=60°,
∴∠BCP=30°,
∵△BCP是由△BCP沿CP折叠得到的,
∴∠B′CP=∠BCP=30°,B′C=BC=4,
∴∠DCB′=90°-30°-30°=30°,
∵B′D⊥OC于点D,
∴∠B′DC=90°,
∴B′D=2,CD=![]() ,
,
∴OD=OC-CD=![]() ,
,
∴点B′的坐标为:![]() .
.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目