题目内容
在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x。
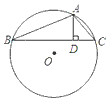
(1)求y关于x的函数关系式;
(2)当AB的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积。
(2)当AB的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积。
解:(1)作直径AE,连接CE,则∠ACE=90°,
∵AD⊥BC,
∴∠ACE=∠ADB,
又∠B=∠E,
∴△ABD∽△AEC,
∴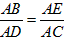 即
即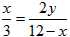 ,
,
∴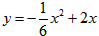 ;
;
(2)当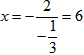 时,y最大为6,
时,y最大为6,
∴⊙O的最大面积为36π。
∵AD⊥BC,
∴∠ACE=∠ADB,
又∠B=∠E,
∴△ABD∽△AEC,
∴
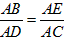 即
即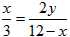 ,
,∴
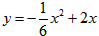 ;
;(2)当
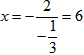 时,y最大为6,
时,y最大为6,∴⊙O的最大面积为36π。

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
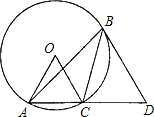 如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )
如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )A、1+
| ||||
B、
| ||||
C、
| ||||
D、
|
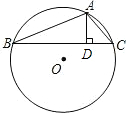 在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x.
在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x.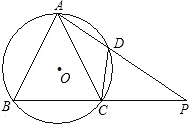 如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.
如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.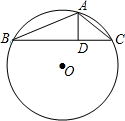 如图,在⊙O的内接△ABC中,AB+AC=12,AD⊥BC于D,且AD=3,当AB=6时,⊙O的面积最大,最大面积是
如图,在⊙O的内接△ABC中,AB+AC=12,AD⊥BC于D,且AD=3,当AB=6时,⊙O的面积最大,最大面积是
