题目内容
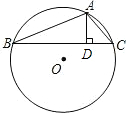 在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x.
在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x.(1)求y关于x的函数关系式;
(2)当AB的长等于多少时,⊙O的面积最大,并求出⊙O的最大面积.
分析:(1)由题意知,需作出圆的直径AE,利用直径所对的圆周角是直角,得出△ABD∽△AEC.根据相似三角形的性质得到边之间的对应比相等,建立函数关系式;
(2)根据二次函数的最值的求法,结合(1)中的函数关系式进行求解.
(2)根据二次函数的最值的求法,结合(1)中的函数关系式进行求解.
解答: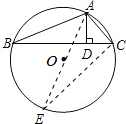 解:(1)作直径AE,连接CE,如图所示,则∠ACE=90°,
解:(1)作直径AE,连接CE,如图所示,则∠ACE=90°,
∵AD⊥BC,∴∠ACE=∠ADB=90度.
又∠B=∠E,
∴△ABD∽△AEC.
∴
=
,即
=
.
整理得y=-
(x-6)2+6.
(2)由(1)知y=-
(x-6)2+6,则当x=6时,y取得最大值,最大值为6.
∴⊙O的最大面积为36π.
 解:(1)作直径AE,连接CE,如图所示,则∠ACE=90°,
解:(1)作直径AE,连接CE,如图所示,则∠ACE=90°,∵AD⊥BC,∴∠ACE=∠ADB=90度.
又∠B=∠E,
∴△ABD∽△AEC.
∴
| AB |
| AD |
| AE |
| AC |
| x |
| 3 |
| 2y |
| 12-x |
整理得y=-
| 1 |
| 6 |
(2)由(1)知y=-
| 1 |
| 6 |
∴⊙O的最大面积为36π.
点评:此题主要考查三角形相似及二次函数最大值的求法.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
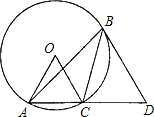 如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )
如图,在⊙O的内接△ABC中,∠ABC=30°,AC的延长线与过点B的⊙O的切线相交于点D,若⊙O的半径OC=1,BD∥OC,则CD的长为( )A、1+
| ||||
B、
| ||||
C、
| ||||
D、
|
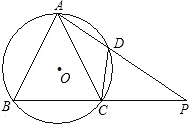 如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.
如图,在⊙O的内接△ABC中,AB=AC,D是⊙O上一点,AD的延长线交BC的延长线于点P.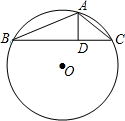 如图,在⊙O的内接△ABC中,AB+AC=12,AD⊥BC于D,且AD=3,当AB=6时,⊙O的面积最大,最大面积是
如图,在⊙O的内接△ABC中,AB+AC=12,AD⊥BC于D,且AD=3,当AB=6时,⊙O的面积最大,最大面积是
