题目内容
【题目】如图,⊙![]() 半径为
半径为![]() ,
, ![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为
为![]() 延长线上一点,动点
延长线上一点,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,同时,动点
方向运动,同时,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,当两点相遇时都停止运动.过点
方向运动,当两点相遇时都停止运动.过点![]() 作
作![]() 的垂线,与⊙
的垂线,与⊙![]() 分别交于点
分别交于点![]() 、
、![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
(![]() )当四边形
)当四边形![]() 是正方形时,
是正方形时, ![]() __________
__________ ![]() ,
, ![]() __________
__________ ![]() .
.
(![]() )当四边形
)当四边形![]() 是菱形且
是菱形且![]() 时,求
时,求![]() 内切圆的半径.
内切圆的半径.
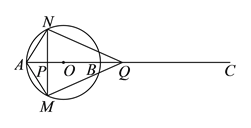
【答案】 ![]()
![]()
【解析】试题分析:(![]() )当四边形
)当四边形![]() 是正方形时,得到
是正方形时,得到![]() ,从而
,从而![]() 与
与![]() 重合
重合![]()
![]() ,得到t的值,进而得到AC的长;
,得到t的值,进而得到AC的长;
(![]() )当四边形
)当四边形![]() 是菱形时,得到AP=PQ,从而得到t的值,进而得到AP,BP的长.通过证明△APN∽△NPB,得到NP的值,进而得到MP,PQ,CQ的值,即可得到
是菱形时,得到AP=PQ,从而得到t的值,进而得到AP,BP的长.通过证明△APN∽△NPB,得到NP的值,进而得到MP,PQ,CQ的值,即可得到![]() 的值,再由
的值,再由![]() ,即可得出结论.
,即可得出结论.
试题解析:解:(![]() )当四边形
)当四边形![]() 是正方形时,此时
是正方形时,此时![]() ,∠NAM=90°,∴MN为直径,故
,∠NAM=90°,∴MN为直径,故![]() 与
与![]() 重合
重合![]() .
.
∵![]() ,∴
,∴![]() ,
, ![]() .
.
(![]() )此时
)此时![]() 即
即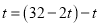 ,解得
,解得![]() ,则
,则![]() ,
, ![]() .
.
∵四边形![]() 是菱形,∴
是菱形,∴![]() .
.
∵![]() 是⊙
是⊙![]() 直径,∴
直径,∴![]() ,∴
,∴![]() ,
,
∴![]() 即
即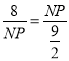 ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
设![]() 内切圆的半径为
内切圆的半径为![]() ,
,
∵![]() ,
,
即![]() ,
, ![]() .
.


练习册系列答案
相关题目