题目内容
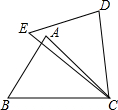
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.

(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.
(1) 证明见解析; (2)∠ACF=60°.
试题分析:(1) 两个直角三角形中,一组直角边和斜边对应相等,两直角三角形全等,由题, ∠ABC=90º,所以∠CBF=90º,在Rt△ABE和Rt△CBF中, AE="CF," AB=BC,所以Rt△ABE≌Rt△CBF(HL).(2) 由题,AB="BC," ∠ABC=90°,所以∠CAB=∠ACB=45°,所以∠BAE=∠CAB-∠CAE=45°-30°=15°,由(1)知道Rt△ABE≌Rt△CBF(HL),所以∠BCF=∠BAE=15°,所以∠ACF=∠BCF+∠ACB=45°+15°=60°.
试题解析:(1) ∵∠ABC=90º,
∴∠CBF=90º,
在Rt△ABE和Rt△CBF中,
AE="CF," AB=BC,
∴Rt△ABE≌Rt△CBF(HL).
(2) 由题,AB="BC," ∠ABC=90°,
∴∠CAB=∠ACB=45°,
∴∠BAE=∠CAB-∠CAE=45°-30°=15°,
由(1)知道Rt△ABE≌Rt△CBF(HL),
∴∠BCF=∠BAE=15°,
∴∠ACF=∠BCF+∠ACB=45°+15°=60°.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
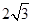 ,则它的边长为( )
,则它的边长为( )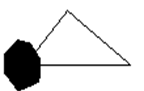
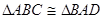 ,AB=6cm,BD=7cm,AD=5cm,则BC的长等于 ( )
,AB=6cm,BD=7cm,AD=5cm,则BC的长等于 ( )