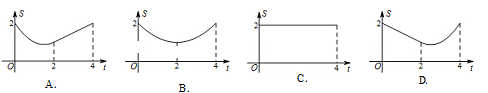题目内容
二次函数y=ax2+bx+c(a≠0)的图象所示,若∣ax2+bx+c∣=k(k≠0)有两个不相等的实数根,则k的取值范围是( )
| A.k<﹣3 | B.k>﹣3 | C.k<3 | D.k>3 |
D.
解析试题分析:∵当ax2+bx+c≥0,y=ax2+bx+c(a≠0)的图象在x轴上方,
∴此时y=|ax2+bx+c|=ax2+bx+c,
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴上方部分的图象,
∵当ax2+bx+c<0时,y=ax2+bx+c(a≠0)的图象在x轴下方,
∴此时y=|ax2+bx+c|=﹣(ax2+bx+c)
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象,
∵y=ax2+bx+c(a≠0)的顶点纵坐标是﹣3,
∴函数y=ax2+bx+c(a≠0)在x轴下方部分与x轴对称的图象的顶点纵坐标是3,
∴y=|ax2+bx+c|的图象如图,
∵观察图象可得当k≠0时,
函数图象在直线y=3的上方时,纵坐标相同的点有两个,
函数图象在直线y=3上时,纵坐标相同的点有三个,
函数图象在直线y=3的下方时,纵坐标相同的点有四个,
∴若|ax2+bx+c|=k(k≠0)有两个不相等的实数根,
则函数图象应该在y=3的上边,
故k>3,
故选D.
考点:1.二次函数的图象2.二次函数的性质.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案点P(a,2)与点Q(3,b)是抛物线y=x2-2x+c上两点,且点P、Q关于此抛物线的对称轴对称,则ab的值为( )
| A.1 | B.-1 | C.-2 | D.2 |
抛物线y=x2﹣2x+3的顶点坐标是( )
| A.(1,﹣2) | B.(1,2) | C.(﹣1,2) | D.(﹣1,﹣2) |
关于二次函数y=2x2+3,下列说法中正确的是( )
| A.它的开口方向是向下 | B.当x<-1时,y随x的增大而减小 | C.它的顶点坐标是(2,3) | D.当x=0时,y有最大值是3 |
数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y= 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )
| A.0<x0<1 |
| B.1<x0<2 |
| C.2<x0<3 |
| D.﹣1<x0<0 |
设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是________.
| A.c=3 | B.c≥3 | C.1≤c≤3 | D.c≤3 |
为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100 m,则池底的最大面积是( )
| A.600 m2 | B.625 m2 | C.650 m2 | D.675 m2 |