题目内容
抛物线y=x2﹣2x+3的顶点坐标是( )
| A.(1,﹣2) | B.(1,2) | C.(﹣1,2) | D.(﹣1,﹣2) |
B.
解析试题分析:已知抛物线的解析式是一般式,用配方法转化为顶点式,根据顶点式的坐标特点,直接写出顶点坐标.
∵y=x2-2x+3=x2-2x+1-1+3=(x-1)2+2,
∴抛物线y=x2-2x+3的顶点坐标是(1,2).
故选B.
考点: 二次函数的性质.

练习册系列答案
相关题目
二次函数y=ax2+bx+c(a≠0)的图象所示,若∣ax2+bx+c∣=k(k≠0)有两个不相等的实数根,则k的取值范围是( )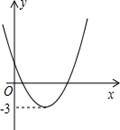
| A.k<﹣3 | B.k>﹣3 | C.k<3 | D.k>3 |
二次函数y=2(x-1)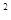 -1的顶点是( ).
-1的顶点是( ).
| A.(1,-1) | B.(1,1) | C.(-1,1) | D.(2,-l) |
二次函数y=2(x+1)2-3的图象的对称轴是( )
| A.直线x=-1 | B.直线x=1 | C.直线x=-3 | D.直线x=3 |
已知抛物线的解析式为y=﹣(x+3)2+1,则它的顶点坐标是( )
| A.(﹣3,1) | B.(3,1) | C.(3,﹣1) | D.(1,3) |
二次函数y=﹣3x2﹣6x+5的图象的顶点坐标是( )
| A.(﹣1,8) | B.(1,8) | C.(﹣1,2) | D.(1,﹣4) |
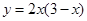 的图象大致是下图的
的图象大致是下图的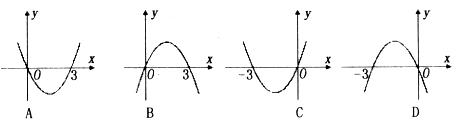
 (x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>﹣1时,y随x的增大而减小,其中正确结论的个数为( )
(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>﹣1时,y随x的增大而减小,其中正确结论的个数为( ) 的图象可能是( )
的图象可能是( )