题目内容
如图,在平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是边AD,AB的中点,EF交AC于点H,则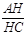 的值为 。
的值为 。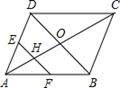
解析试题分析:因为点E、F分别是边AD,AB的中点,所以EF是三角形ABD的中位线,根据三角形中位线的性质,EF∥BD,所以△AEH∽△ADO,所以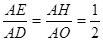 ,再根据平行四边形的性质:平行四边形的对角线互相平分.可得AO=CO,所以
,再根据平行四边形的性质:平行四边形的对角线互相平分.可得AO=CO,所以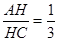 .
.
考点:1、平行四边形的性质;2、相似三角形的性质.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 .
.
 中,点
中,点 、
、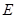 分别在边
分别在边 、
、 上,
上, 平分
平分 ,
,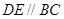 ,如果
,如果 ,
, ,那么
,那么 .
.

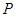 是线段
是线段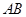 的黄金分割点,
的黄金分割点,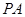 >
>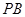 ,且
,且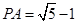 ,则
,则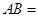 .
. 的值,并说明理由.
的值,并说明理由.
