Question

【题目】如图，Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=1，将△ABC绕点C逆时针旋转至△CDE，使得点D恰好落在AB上，连接BE，则BE的长度为 ．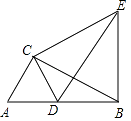

Answer 1

【答案】
【解析】解：∵Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=1，

∴AB=2，BC= ，

∵∠A=60°，将△ABC绕点C逆时针旋转至△CDE，

∴AC=DC，

∴△ADC是等边三角形，

∴AD= AB=1，

∴DC=DB，

∴∠DCB=∠DBC=30°，

∵△CDE是△ABC旋转而成，

∴∠DCE=90°，BC=EC，

∴∠ECB=90°﹣30°=60°，

∴△BCE是等边三角形，

∴BE=BC= ．

所以答案是： ．

【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识，掌握在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半，以及对旋转的性质的理解，了解①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．