题目内容
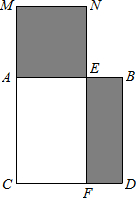如图，已知线段AB的长为1，以AB为边在AB下方作正方形ACDB．取AB边上一点E，以AE为边在AB的上方作正方形AENM．过E作EF⊥CD，垂足为F点．若正方形AENM与四边形EFDB的面积相等，设AE=x，可列方程为x2=1-x
x2=1-x
．分析：本题需先设出AE的长，从而得出BE的长，再根据题意列出方程，求出x的值即可得出AE的长．
解答：解：设AE的长为x，则BE的长为1-x，
又∵四边形ABCD是正方形，
∴BD=AB=1，
由题意得得：x2=1-x．
故答案为：x2=1-x．
又∵四边形ABCD是正方形，
∴BD=AB=1，
由题意得得：x2=1-x．
故答案为：x2=1-x．
点评：本题主要考查了根据实际问题列一元二次方程的知识，在解题时要根据已知条件和图形列出方程是本题的关键．
练习册系列答案
相关题目
如图，已知线段AB的长为2.8cm．
如图，已知线段AB的长度是acm，线段BC的长度比线段AB长度的2倍多5cm，线段AD的长度比线段BC长度的2倍少5cm．