Question

如图，已知∠1＋∠2＝180º，∠DAE＝∠BCF．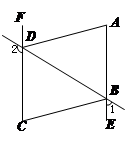

（1）试判断直线AE与CF有怎样的位置关系？并说明理由；
（2）若∠BCF＝70º，求∠ADF的度数；
（3）若DA平分∠BDF，请说明BC平分∠DBE．

Answer 1

（1）AE∥CF（2）70°（3）可通过证明∠ADF=∠ADB∠DBC=∠CBE，则BC平分∠DBE

解析试题分析：（1）∵∠1+∠2=180°，∠BDC+∠2=180°  ∴∠1=∠BDC ∴AE∥CF   
（2）∵AE∥CF  ∴∠BCF=∠CBE 又∵∠DAE=∠BCF   ∴∠DAE=∠CBE  
∴AE∥CF  ∴∠ADF=∠BCF=70°  
（3）∵AD∥BC，AE∥CF  ∴∠ADB=∠DBC，∠ADF=∠A   
∵∠CBE=∠A   ∴∠ADF=∠CBE 
又∵DA平分∠BDF ∴∠ADF=∠ADB
∴∠DBC=∠CBE，则BC平分∠DBE．  
考点：平行线性质及判定
点评：本题难度中等，主要考查学生对平行线性质和判定知识点的掌握，结合角平分线性质综合运用解决几何问题。为中考常考题型，要求学生培养数形结合思想，运用到考试中去。