题目内容
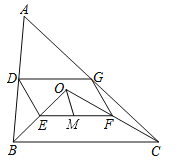
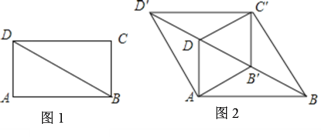
【题目】如图1,BD是矩形ABCD的对角线,![]() ,
,![]() .将
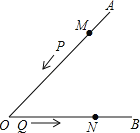
.将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,连接
的位置,连接![]() ,
,![]() ,
,![]() ,
,![]() ,如图2.
,如图2.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形,请说明理由;
是菱形,请说明理由;
(3)在(2)的条件下,将四边形![]() 沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形,直接写出所有可能拼成的矩形周长.
【答案】(1)见解析;(2)当![]() 运动到BD中点时,四边形
运动到BD中点时,四边形![]() 是菱形,理由见解析;(3)
是菱形,理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)根据平行四边形的判定定理一组对边相等一组对角相等,即可解答
(2)有一组邻边相等的平行四边形是菱形,据此进行证明即可;
(3)根据两种不同的拼法,分别求得可能拼成的矩形周长.
(1)∵BD是矩形ABCD的对角线,![]() ,
,
∴![]() ,
,
由平移可得,![]() ,
,
![]() ,
,
∴![]()
∴四边形![]() 是平行四边形,
是平行四边形,
(2)当![]() 运动到BD中点时,四边形
运动到BD中点时,四边形![]() 是菱形
是菱形
理由:∵![]() 为BD中点,
为BD中点,
∴![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴四边形![]() 是菱形;
是菱形;
(3)将四边形ABC′D′沿它的两条对角线剪开,用得到的四个三角形拼成与其面积相等的矩形如下:
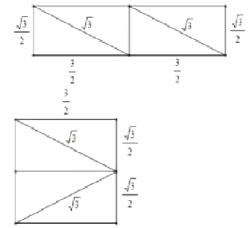
∴矩形周长为![]() 或
或![]() .
.

 春雨教育同步作文系列答案
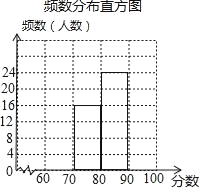
春雨教育同步作文系列答案【题目】九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”知识竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
频数分布表
分数段 | 频数(人数) |
60≤x<70 | a |
70≤x<80 | 16 |
80≤x<90 | 24 |
90≤x<100 | b |
请解答下列问题:
(1)完成频数分布表,a= ,b= .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.