题目内容
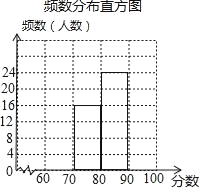
【题目】九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”知识竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
频数分布表
分数段 | 频数(人数) |
60≤x<70 | a |
70≤x<80 | 16 |
80≤x<90 | 24 |
90≤x<100 | b |
请解答下列问题:
(1)完成频数分布表,a= ,b= .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
【答案】(1)4,4;(2)答案见解析(3)估计该校成绩90≤x<100范围内的学生有50人(4)![]()
【解析】试题分析:(1)将余下的8位同学按60≤x<70、90≤x<100分组可得a、b的值;
(2)根据(1)中所得结果补全即可得;
(3)将样本中成绩90≤x<100范围内的学生所占比例乘以总人数600可得答案;
(4)画树状图列出所有等可能结果,根据概率公式求解可得.
试题解析:(1)由题意知,60≤x<70的有60、63、67、68这4个数,90≤x<100的有90、99、99、99这4个,即a=4、b=4,故答案为:4,4;
(2)补全频数分布直方图如下:
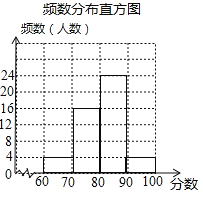
(3)600×![]() =50(人).
=50(人).
答:估计该校成绩90≤x<100范围内的学生有50人.
(4)画树状图得:
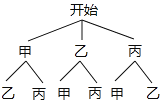
∵共有6种等可能的结果,甲、乙被选中的有2种情况,∴甲、乙被选中的概率为![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目