题目内容
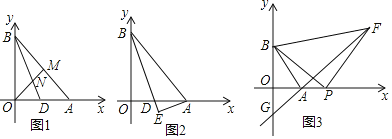
【题目】在△ABC中,∠ABC,∠ACB的平分线交于点O,D是外角与内角平分线交点,E是外角平分线交点,若∠BOC=120°,则∠D=_____;∠E=_____.

【答案】30°; 60°.
【解析】
根据角平分线的定义、三角形内角和定理进行计算即可.
∵BO平分∠ABC,CO平分∠ACB,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∵∠ABC+∠ACB+∠A=180°,
∴2∠OCB+2∠OBC+∠A=180°,
∴∠OCB+∠OBC=90°﹣![]() ∠A,
∠A,
∵∠OCB+∠OBC+∠BOC=180°,
∴90°﹣![]() ∠A+∠BOC=180°,
∠A+∠BOC=180°,
∴∠BOC=90°+![]() ∠A,
∠A,
而∠BOC=120°,
∴∠A=60°,
∵∠DCF=∠D+∠DBC,∠ACF=∠ABC+∠A,BD平分∠ABC,DC平分∠ACF,
∴∠ACF=2∠DCF,∠ABC=2∠DBC,
∴2∠D+2∠DBC=∠ABC+∠A,
∴2∠D=∠A,即∠D=![]() ∠A.
∠A.
∵∠A=60°,
∴∠D=30°,
∵∠ABC,∠ACB的平分线交于点O,E是外角平分线交点,
∴∠OBE=∠OCE=90°,
∴∠E=180°﹣(∠OBE+∠D)= 180°﹣120°=60°,
故答案为:30°;60°.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目