题目内容
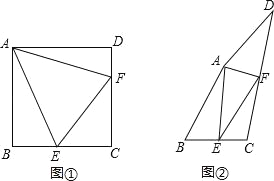
【题目】探究:如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连结EF,求证:EF=BE+DF.
应用:如图②,在四边形ABCD中,点E、F分别在BC、CD上,AB=AD,∠B+∠D=90°,∠EAF=![]() ∠BAD,若EF=3,BE=2,则DF= .
∠BAD,若EF=3,BE=2,则DF= .
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)如图①中,把△ABE绕点A逆时针旋转90°得到△ADE′,只要证明△AFE≌△AFE′即可解决问题.
(2)如图②中,将△ABE绕点A旋转到△ADE′位置连接E′F.,只要证明△FAE≌△FAE′得EF=FE′,在RT△E′DF中利用勾股定理即可解决问题.
试题解析:(1)如图①中,
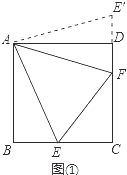
在正方形ABCD中,∵AB=AD,∠BAD=∠ADC=∠B=90°,
把△ABE绕点A逆时针旋转90°得到△ADE′,
∵∠ADF=∠ADE′=90°,
∴点F、D、E′共线,
∴∠E′AF=90°-45°=45°=∠EAF,
在△AFE和△AFE′中,
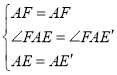 ,
,
∴△AFE≌△AFE′,
∵EF=FE′=DE′+DF=DE+DF.
(2)如图②中,
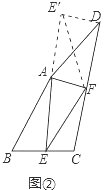
因为AB=AD,所以可以将△ABE绕点A旋转到△ADE′位置,连接E′F.
∵∠B+∠ADF=90°,∠B=∠E′DA,
∴∠E′DF=∠E′DA+′ADF=90°,
∵∠BAE+∠DAF=∠EAF,∠E′AD=∠BAE,
∴∠E′AF=∠EAF,
在△FAE和△FAE′中,
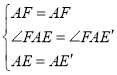 ,
,
∴△FAE≌△FAE′,
∴EF=FE′=3,
在RT△E′DF中,∵∠E′DF=90°,E′F=3,DE′=BE=2,
∴DF=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目