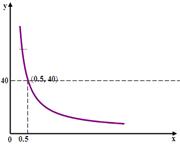
题目内容
已知一个反比例函数的图象经过点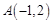 .
.
(Ⅰ)求这个函数的解析式;
(Ⅱ)判断点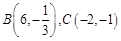 是否在这个函数的图象上;
是否在这个函数的图象上;
(Ⅲ)当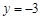 时,求自变量
时,求自变量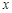 的值.
的值.
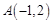 .
.(Ⅰ)求这个函数的解析式;
(Ⅱ)判断点
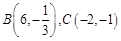 是否在这个函数的图象上;
是否在这个函数的图象上;(Ⅲ)当
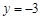 时,求自变量
时,求自变量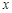 的值.
的值.(Ⅰ)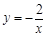 ;(Ⅱ)
;(Ⅱ)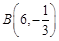 在,点
在,点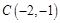 不在;(Ⅲ)
不在;(Ⅲ)
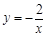 ;(Ⅱ)
;(Ⅱ)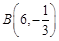 在,点
在,点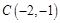 不在;(Ⅲ)
不在;(Ⅲ)
试题分析:(Ⅰ)设这个函数的解析式为
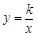 ,由图象经过点
,由图象经过点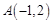 根据待定系数法即可求得结果;
根据待定系数法即可求得结果;(Ⅱ)分别把
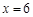 与
与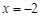 代入(Ⅰ)中的解析式,根据计算结果即可作出判断;
代入(Ⅰ)中的解析式,根据计算结果即可作出判断;(Ⅲ)直接把
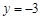 代入(Ⅰ)中的解析式即可求得结果.
代入(Ⅰ)中的解析式即可求得结果.(Ⅰ)设这个函数的解析式为
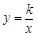
依题意得,
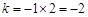 ,
,∴ 这个函数的解析式为
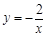 ;
; (Ⅱ)当
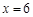 时,
时,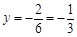 ,故点
,故点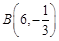 在这个函数的图象上;
在这个函数的图象上;当
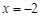 时,
时,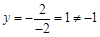 ,故点
,故点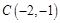 不在这个函数的图象上;
不在这个函数的图象上;(Ⅲ)当
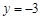 时,
时,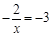 ,
,解得,
 .
.点评:待定系数法求函数解析式是初中数学的重点,贯穿于整个初中数学的学习,是中考的热点,在各类题型中均有出现,要熟练掌握.

练习册系列答案
相关题目
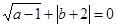 ,点M
,点M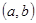 在反比例函数
在反比例函数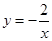 的图象上,则反比例函数的解析式为( )
的图象上,则反比例函数的解析式为( )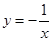
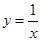
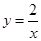
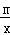 的图象相交于点A(﹣1,2)、点B(﹣4,n)
的图象相交于点A(﹣1,2)、点B(﹣4,n)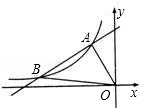
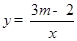 ,当
,当 时,其图象的两个分支在第一、三象限内;当
时,其图象的两个分支在第一、三象限内;当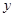 随
随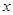 的增大而增大;
的增大而增大;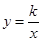 的图象经过点
的图象经过点 .
.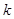 的值;
的值; 取什么值时,函数的值大于0?
取什么值时,函数的值大于0?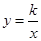 与
与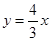 相交于A,B两点,且A(3,4)过A作AC⊥x轴于C点,
相交于A,B两点,且A(3,4)过A作AC⊥x轴于C点,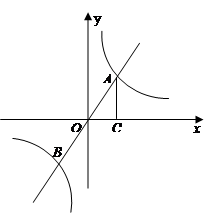
 的图象位于( )
的图象位于( )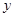 (min)与装载速度
(min)与装载速度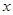 (t/min)之间的函数关系如图:
(t/min)之间的函数关系如图: