题目内容
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。

1.(1)求经过A、B、C三点的抛物线的表达式;
2.(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1与△OAB对应线段的比为3:1,请在右图网格中画出放大后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
3.(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平移得到?请说明理由。
【答案】
1.(1)设经过A、B、C三点的抛物线的表达式y=a(x-1)(x+1),
∵经过(0,1), ∴1=a(-1)×1
∴a=-1;∴y=-1×(x-1) (x+1)=-x2+1;(3分)
2.(2)如图所示(5分)
 |
3.(3)设经过A1、B1、C1三点的抛物线为:y=a(x-2)2+5。
把(5,2)代入可得a=-13 ∴y=-13(x-2)2+5
∵和(1)得到的二次项系数不同 ∴不能通过平移到(10分)
【解析】略

练习册系列答案
相关题目
 .
.

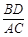 的值.
的值.