题目内容
如图1,已知直线y=-| 1 |
| 2 |
| k |
| x |
(1)若OE•CE=12,求k的值.
(2)如图2,作BF⊥y轴于F,求证:EF∥CD.
(3)在(1)(2)的条件下,EF=
| 5 |
| 5 |
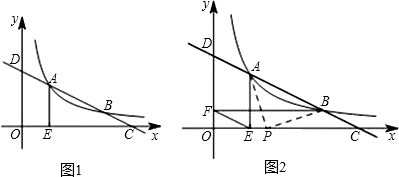
分析:(1)分别设出一次函数解析式和反比例函数的解析式,代入点A的坐标,即可得出各解析式.
(2)连接AF、BE,过E、F分别作FM⊥AB,EN⊥AB,得出FM∥EN,再根据AE⊥x轴,BF⊥y轴,得出AE⊥BF,由此得出S△AEF=S△BEF,最后证出FM=EN,得出四边形EFMN是矩形,由此证出EF∥CD;
(3)由(2)得出EF=AD=BC和CD的值,再由直线解析式可得OD=m,OC=2m,得出OD=4,再根据EF∥CD,得出OF和0E、DF的值,最后根据EF=
,AB=2
得出EP的值,即可求出P点的坐标;
(2)连接AF、BE,过E、F分别作FM⊥AB,EN⊥AB,得出FM∥EN,再根据AE⊥x轴,BF⊥y轴,得出AE⊥BF,由此得出S△AEF=S△BEF,最后证出FM=EN,得出四边形EFMN是矩形,由此证出EF∥CD;
(3)由(2)得出EF=AD=BC和CD的值,再由直线解析式可得OD=m,OC=2m,得出OD=4,再根据EF∥CD,得出OF和0E、DF的值,最后根据EF=
| 5 |
| 5 |
解答:(1)解:设OE=a,则A(a,-
a+m),
∵点A在反比例函数图象上,∴a(-
a+m)=k,即k=-
a2+am,
由一次函数解析式可得C(2m,0),
∴CE=2m-a,
∴OE.CE=a(2m-a)=-a2+2am=12,
∴k=
(-a2+2am)=
×12=6.
(2)证明:连接AF、BE,过E、F分别作FM⊥AB,EN⊥AB,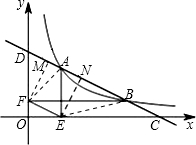
∴FM∥EN,
∵AE⊥x轴,BF⊥y轴,
∴AE⊥BF,
S△AEF=
AE•OE=
,
S△BEF=
BF•OF=
,
∴S△AEF=S△BEF,
∴FM=EN,
∴四边形EFMN是矩形,
∴EF∥CD;
(3)解:由(2)可知,EF=AD=BC=
,
∴CD=4
,
由直线解析式可得OD=m,OC=2m,
∴OD=4,
又EF∥CD,
∴OE=2OF,
∴OF=1,0E=2,
∴DF=3,
∴AE=DF=3,
∵AB=2
,
∴AP=
,
∴EP=1,
∴P(3,0).
| 1 |
| 2 |
∵点A在反比例函数图象上,∴a(-
| 1 |
| 2 |
| 1 |
| 2 |
由一次函数解析式可得C(2m,0),
∴CE=2m-a,
∴OE.CE=a(2m-a)=-a2+2am=12,
∴k=
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明:连接AF、BE,过E、F分别作FM⊥AB,EN⊥AB,

∴FM∥EN,
∵AE⊥x轴,BF⊥y轴,
∴AE⊥BF,
S△AEF=
| 1 |
| 2 |
| k |
| 2 |
S△BEF=
| 1 |
| 2 |
| k |
| 2 |
∴S△AEF=S△BEF,
∴FM=EN,
∴四边形EFMN是矩形,
∴EF∥CD;
(3)解:由(2)可知,EF=AD=BC=
| 5 |
∴CD=4
| 5 |
由直线解析式可得OD=m,OC=2m,
∴OD=4,
又EF∥CD,
∴OE=2OF,
∴OF=1,0E=2,
∴DF=3,
∴AE=DF=3,
∵AB=2
| 5 |
∴AP=
| 10 |
∴EP=1,
∴P(3,0).
点评:此题考查了反比例函数的综合题;解题的关键是画出图象,找出对应关系;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
相关题目
 如图1,已知直线:
如图1,已知直线: