题目内容
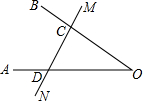
如图，点O，A，B在同一直线上，OC平分∠AOD，OE平分∠FOB，∠COF=∠DOE=90°，求∠AOD．
∵∠COF=∠DOE=90°，
∴都减去∠DOF得：∠DOC=∠FOE，
∵OC平分∠AOD，OE平分∠FOB，
∴∠AOC=∠COD=∠BOE=∠EOF，
∵∠DOE=90°，
∴∠COA+∠COD+∠BOE=90°，
∴∠AOC=∠COD=∠BOE=∠EOF=30°，
∴∠AOD=2×30°=60°．
∴都减去∠DOF得：∠DOC=∠FOE，
∵OC平分∠AOD，OE平分∠FOB，
∴∠AOC=∠COD=∠BOE=∠EOF，
∵∠DOE=90°，
∴∠COA+∠COD+∠BOE=90°，
∴∠AOC=∠COD=∠BOE=∠EOF=30°，
∴∠AOD=2×30°=60°．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
