题目内容
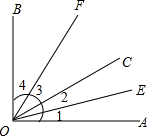
如图，点A、O、E在同一直线上，∠AOB=50°，∠EOD=27°，OD平分∠COE，求∠COB的度数．
∵OD平分∠COE，
∴∠EOC=2∠EOD=2×27°=54°，
又∵∠AOE=∠AOB+∠COB+∠EOC，
而且点A、O、E在同一直线上，
∴∠AOE=180°，
∴∠COB=∠AOE-∠AOB-∠EOC=180°-50°-54°=76°．
∴∠EOC=2∠EOD=2×27°=54°，
又∵∠AOE=∠AOB+∠COB+∠EOC，
而且点A、O、E在同一直线上，
∴∠AOE=180°，
∴∠COB=∠AOE-∠AOB-∠EOC=180°-50°-54°=76°．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
